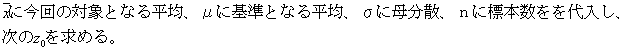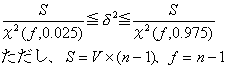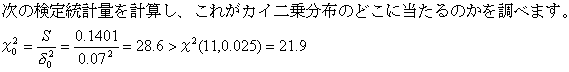第５回　種々の統計的推定と検定：ｔ検定・Ｆ検定・カイ二乗検定

　標本平均は標本の大きさが十分に大きければ正規分布に従う。そこで正規分布の性質から標本から得た統計量を利用して、母集団に関する統計的な検定をすることができます。
　例えば、次の例を考えてみましょう。

例：　枕木養鶏舎では平均45gの卵を集荷している。枕木山の木を伐採し、鶏舎の日当たりをよくした。その結果、卵100個を調査すると、平均47g、標準偏差5gとなった。卵の重さは変化したのだろうか。

１．帰無仮説を設定する。
　前回、学んだように統計的検定でできるのは仮説の反証を示すことだけです。ここで仮説は検証可能な仮説である卵の重さに変化はなかったということです。卵の重さに変化はなかったのにもかかわらず、今回のデータを得る確率はいくらかを計算し、その確率がある一定の確率以下であれば、元の仮説（帰無仮説）がむしろ間違っていると判断し、対立仮説（卵の重さは変化したあるいは増加した）を採用するのです。
　このように統計的検定では帰無仮説に対する反証を示すことで対立仮説が正しいとする方法をとります。

２．必要なデータは何かを確認する。　
　まず、帰無仮説は卵の重さは変わらなかったというのですから、卵の重さの平均は45g、標準偏差は5gということになります。一方、今回のデータは卵の重さの平均は47gです。データの数は100個です。従いまして、今回のデータの卵の重さの標準誤差は
　

このｚ₀は標準正規分布に従います。したがって、ｚ₀の絶対値が1.96より大きくなる確率は5％であり、2.576より大きくなる確率は1％です。今回のデータからはｚ₀は4となりましたから、このようなｚ0を得る確率は1％よりも小さく、帰無仮説が正しいとするとめったに起こらないことになります。したがって、帰無仮説（卵の重さは変わらなかった）の反証が示されたと考え、帰無仮説は棄却され、対立仮説を採用します。

４．もう一つの検定の仕方
　３．のやり方はコンピューターの利用が困難で、標準正規分布の表を見て、検定する時代のものでした。今では、だれでも容易にコンピューターで正規分布に関する計算ができますから、むしろ次のように検定する方がよいでしょう。

５．片側検定
例：B牧場では牛の餌をF社からG社に変えた。G社の餌はより栄養価が高いので、F社のときの泌乳量5.0L、標準偏差0.8Lより向上すると予想した。実際に100頭を調査した結果、泌乳量は5.2Lとなった。泌乳量は増加したか？

帰無仮説：　泌乳量は5Lである。
対立仮説：　泌乳量は5Lより増加した。

前項では、標本が十分に大きいあるいは母分散が既知であることを条件に正規分布を用いて、検定しました。しかし、標本数が少ないときは母分散を標本の分散から推定する誤差があるために、その不確実さを加味したｔ分布によって、推定・検定しなければいけない。
ｔ分布を用いた推定と検定の具体的な方法は授業に譲るとして、ここではエクセルを用いた方法を紹介します。

対応のない２つの小標本に関するｔ検定では２つの標本の分散が等しいことが条件として求められます。２つの標本の分散が等しいかを検定するのはＦ検定でできます。もし２つの標本の分散が異なる場合はWelchの検定によって、２つの小標本の平均を検定します。Welchの検定については授業では説明しませんでしたが、エクセルではｔ検定同様に簡単に検定できます。

カイ二乗分布
　母分散が既知の時に標本の分散がどのような分布を示すかを表すのがカイ二乗分布です。カイ二乗分布は自由度だけで決定し、母分散の値σ^２は関与しません。

カイ二乗分布を使った分散の区間推定
　カイ二乗分布を利用すると、標本から得られた分散を利用して、母分散を区間推定することができます。

95％の信頼区間で母分散を推定する場合、
平方和をＳ、自由度をｆ、サンプル数をｎ、標本の分散をＶとすると
母分散σ^２は次の区間に９５％の確率で入る。

カイ二乗分布を用いて、ある標本の分散がある値であるかということを検定できます。
例：Ｋ牧場の牛の乳脂肪率の標準偏差は0.07%であった。新しい飼育法の導入で乳脂肪率にばらつきが変化したかを知りたい。12頭を無作為に調査した結果配下の通りである。
7.02,7.03,6.82,7.08,7.13,6.92,6.87,7.02,6.97,7.08,7.19,7.15

以上のことから帰無仮説（分散は変化しなかった）は５％の危険率で棄却されました。したがって、乳脂肪率の分散は変化したと結論できました。

Ｆ分布は２つの標本の分散の比に関する分布を示します。２つの標本それぞれの自由度からＦ分布が決まります。次回の授業から学ぶ分散分析ではＦ分布を利用するので、大切な分布です。なかなか意味をとらえにくい分布かもしれません。

Ｆ分布を利用して２つの標本の分散比を区間推定することもできますが、授業では省略しました。
Ｆ分布を利用した２つの標本の分散に差があるのかを検定できます。この手法は次回から学ぶ分散分析の基礎となります。

例：Ａ，Ｂ２種類の飼料を与えて一定期間飼育したハムスターの体重の増加量を測定した結果、次のような結果を得た。飼料による体重増加量のばらつきに差があるのかを検定せよ。

飼料Ａ　分散5.34、飼料B　分散3.28であるから
分散比（１よりおおきくなるように） 1.63
F値はここではF(9,8;0.025)=4.36であり、帰無仮説は棄却できません。
したがって、５％の有意水準では飼料のばらつきに差があるとはいえないと結論できます。

１．第３回の宿題で卵10個入りについて２つのスーパーで調査した。ｔ分布を用いて、２つのスーパーの卵それぞれの平均について、95％信頼区間をつけて、区間推定せよ。さらに２つのスーパーの卵の重さが同じであるかを危険率１％で検定せよ。

２．１．のデータを用いて、卵の重さのばらつきが同じであるかを危険率５％で検定せよ。また、それぞれの卵について、その母標準偏差を95％信頼区間をつけて、推定せよ。

３．カイ二乗分布は今回学んだように母分散に関する推定・検定に使う。それ以外に、ある標本分布が期待される標本分布に適合しているかを検定するときに使われる。例えば、さいころの６つの目は均等に出現すると期待されるから、その分布は矩形分布（一様分布）と期待できる。しかし、実際に得た分布は必ずしも矩形分布になるとは限らない。そこで、カイ二乗分布によって、実際に得た分布が矩形分布であるのか、ないのかを検定できる。
　次のいくつかの分布のうち１つを選んで実際に調査せよ。ヒストグラムを書いて、目で見た感じでは期待される分布と一致しているのかを考えて見よ。

ｂ．全く実力の同じ者が勝負をすれば、勝つ確率は２分の１であるといえる。逆に実力が違えば、勝つ確率はその実力差に応じて変わると考えられる。このときｎ回勝負したときに、ｘ回勝つ確率は二項分布に従うと見なせる。
　２人で行う勝負（じゃんけん、将棋、相撲なんでもよい）を20回以上行え。もし実力が同じだとした場合、その結果の得られる確率を求めよ。その確率から、両者の実力に差があるのか、ないのかを考えて見よ。（２人１組の班で調査してもかまわない。相手がコンピューターでもよい）

ａ．２つの別々のスーパーから10個入りの卵（Ｍ寸）を買い、両店の卵の重さは同じなのかを調べる。ここでは、卵の重さをはかり、平均と標準偏差を計算する。ここで得た平均と標準偏差から正規分布となる母集団のグラフをだいたいで書いてみる。そこから両店の卵の重さが同じかを考えて見よ。（同じようなデータであれば、卵でなくてもよい。複数の人間で班をつくって、調査してかまわない。）

３．次回の授業ではあるデータが正規分布あるいは二項分布に基づくと仮定して、統計的に推定あるいは検定を行う。例えば、平均ｍ、標準偏差σの正規分布では平均から３σ以上離れた値の出現する確率は0.3％しかない。このことから逆にそのような値が得られたら、元の平均と標準偏差が怪しいと考えることもできる。このような考え方を統計的推定あるいは検定という。