２．回帰分析における推定と検定
　回帰分析で得られた回帰直線も統計量ですから、母集団の回帰直線である母回帰直線（その傾きが母回帰係数）を考えることができます。さらに母回帰係数や母切片についての統計的推定・検定が可能です。
　母回帰係数などに関する推定や検定の数式を覚える必要はありませんが、推定のもつ統計的な意味を把握することは大切です。統計的検定は母回帰係数や母切片であればエクセルでもできます。

３．推定と予測
　回帰分析の目的の一つは独立変数ｘとしてある値が与えられたときに、従属変数ｙがどのような値になるかを知ることです。この場合、ｙの母平均を知りたい場合とｙの個々の実現する値を知りたい場合とがあります。
　ｙの母平均を統計的に見積もることを推定といいます。例えば、10日間道路に走る車の数を調査して、この道路に走る平均の車の数を推定したり、この１日平均の走行数を１ヶ月や１年単位に換算する場合、ｙの母平均を推定していることになります。
　一方、10日間の道路に走る車の数を調査した結果から、ある一日の車の数を知りたいこともあります。例えば、マラソン大会を行うのでどのくらいの車が通行するかを知りたいというような場合です。このように、独立変数ｘに対してｙの実際に実現する値を知ろうとすることを予測といいます。
　そして、推定と予測では点推定・点予測のときは同じ結果を得ますが、信頼区間をつけると、推定では標本数が増えれば増えるほど、推定の信頼区間は0に近づきますが、予測の場合、もともとｙのもつ誤差より精度よく予測はできません。

４．推定の信頼区間はどうなるか？
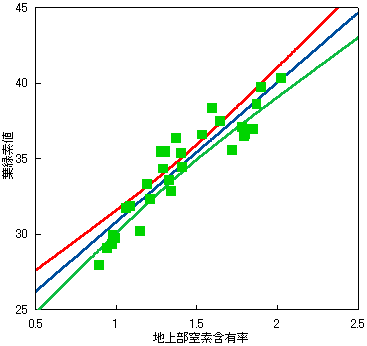
　植物体の地上部窒素含有率は葉の葉緑素値と深い関わりがあります。独立変数ｘを地上部窒素含有率、従属変数ｙを葉緑素値としたときに両者の関係は以下のようなグラフで表せたとしましょう。ここで四角の記号は実際に測定で得られた値であり、図中の青色の直線（回帰式）を求めるのに使った標本データです。

　この図で赤色の線は推定した母平均の95％上側信頼区間、緑色の線は95％下側信頼区間を示します。信頼区間からわかるように標本の平均に近いところでは信頼区間の幅が小さく、データの端になるとかなり信頼区間の幅が広くなっていることがわかります。
　このことから回帰分析では回帰式を求めたデータより外側を推定しようとすると誤差が大きくなることがわかります。過去何年間かの傾向から今後どうなるかを考えるような時間的な傾向を回帰分析で求めるときに、予想が外れやすいのはこのようなことも理由の一つにあげられます。

５．予測の信頼区間はどうなるか？
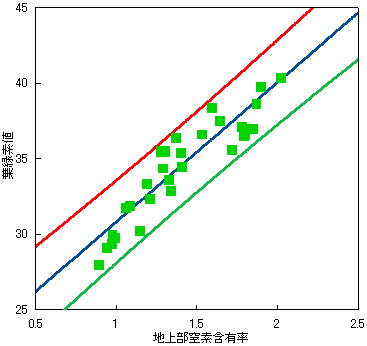
　上のグラフでは回帰式から母平均を推定したときに、推定した母平均の信頼区間はどうなるかを示しました。今度は予測の信頼区間はどうなるでしょうか。ある１つの植物の地上部窒素含有率がわかったとしたらその葉の葉緑素値はどの程度の信頼をもって予測できるでしょうか。その信頼区間は下のグラフのようになります。

　このように予測の信頼区間は推定に比べてずっと大きくなります。なぜなら、ｙはもともと正規分布すると仮定していますから、その正規分布で与えられた誤差より精度よくはならないからです。予測の場合も平均に近いところほど信頼区間は狭く、データの端では信頼区間は広くなります。

６．回帰の逆推定
　上のグラフでは地上部窒素含有率から葉緑素値を計算することになっています。ところが葉緑素値がわかったときに地上部窒素含有率を知りたいということもあります。この場合、葉緑素値を独立変数ｘに、地上部窒素含有率を従属変数ｙにして回帰分析したらよいのでしょうか？これは実は誤りです。回帰分析では独立変数ｘは指定できる値、従属変数ｙはｘが決まればある誤差をともなって決定する値であるという仮定があります。植物では葉緑素値が決まってから、地上部窒素含有率が決まるわけではなく、地上部窒素含有率が葉緑素値を決めていると考える方が自然ですから、独立変数ｘは地上部窒素含有率であるほうがよいでしょう。こうして回帰式を決めてから、今度はこの回帰式をｘについて解き、ｙがわかっているときにｘがどのような値を取るかを逆算します。これを回帰の逆推定といいます。
　化学分析の時に標準液を使って吸光度と濃度の関係を回帰分析してから、未知試料の濃度を求めるのも回帰の逆推定です。この場合も濃度が決まれば吸光度が決まるのであって、吸光度が濃度を決めるのではないので、濃度が独立変数でなければなりません。
　回帰の逆推定でも信頼区間を求めることができます。ただしものすごく煩雑なので、それほど正確に知る必要がなければ上の予測に関するグラフの信頼区間から逆算してもかまいません。予測を用いるのは逆推定で使うｙはある実現した１回きりの値であって、母平均ではないからです。逆推定で使うｙを数回測定してから逆推定する場合は信頼区間を小さくできますが、煩雑すぎるのでここでは紹介するにとどめます。

７．重回帰分析
　単回帰分析では一つの説明変数（独立変数）で目的変数（従属変数）を説明しようとしました。しかし、現実にはいくつかの要因が関与して、ある一つの現象が決まるものはたくさんあります。例えば、水稲の収量は環境要因だけでも、気温、降水量、日射量、風速、湿度などが関与していると考えられます。これらの要因のうち、ある要因はかなり強く収量を支配し、ある要因はそれほど強くは支配していないかもしれません。このように目的変数を説明する説明変数を複数取り上げたいときには重回帰分析を行うことができます。
　重回帰分析は単回帰分析を拡張したものなので、単回帰分析と同じように目的変数は正規分布し、しかもその誤差は説明変数に依存しないことが前提条件となります。さらに説明変数自身は指定できる値であり、誤差を持たないことも前提条件となります。
　重回帰分析の計算はコンピューターでします。エクセルでも可能です。

８．宿題
Ａ．第１０回の宿題で集めた回帰のデータについて以下の計算をせよ。
（１）　回帰係数について95％信頼区間を求めよ。
（２）　回帰係数について、母回帰係数が0であるという帰無仮説の元で5％の有意水準で検定せよ。
（３）　指定したｘについてｙの母平均がどんな値を取るかを計算せよ。さらに推定値の95％信頼区間を計算せよ。指定したｘの値は前回の宿題の講評の一番最後に書いておく。
（４）　指定したｘ（（３）と同じ値）についてｙを予測せよ。さらに予測値の95％信頼区間を計算せよ。
（５）　指定したｙについて、ｘを逆推定せよ。逆推定は点推定でよい。指定したｙの値は前回の宿題の講評の一番最後に書いておく。

Ｅ．エクセルによる回帰分析
　エクセルを使うと、回帰係数、切片だけでなく、回帰の分散分析、回帰係数の有意差検定、母回帰係数の区間推定などもできます。

D．回帰分析における検定
　相関分析では母相関係数ρ＝０という帰無仮説を検定し、この帰無仮説を棄却できれば両変数間に相関があると判断しました。一方、回帰分析では回帰係数が０という帰無仮説を検定します。回帰分析の分散分析で有意となれば、回帰係数は０ではないことになりますから、独立変数ｘを変えれば従属変数ｙが変わることになります。
　数学的には２つの変量について母相関係数ρ＝０の帰無仮説が棄却できるならば、回帰係数＝０の帰無仮説も棄却できます。しかし、統計的には相関と回帰では意味が異なります。

C．回帰分析の手順
　回帰式（回帰係数と切片）を求める→分散分析を行う→分散分析の結果、回帰による変動が有意であれば、必要に応じて、回帰係数や切片の推定・検定を行う

B．回帰分析では何を求めるか？
　回帰分析では独立変数ｘに対してｙがいくつになるかを表す式（回帰式）を求めます。直線の回帰式であれば、その傾き（回帰係数）とその切片を求めれば回帰式が求まります。

１．回帰分析
A．相関係数
　回帰の時でも相関係数を計算できます。ただし母相関係数に関する推定や検定はできません。さらに回帰では相関係数を二乗した値である寄与率の方がより重要な評価基準となります。