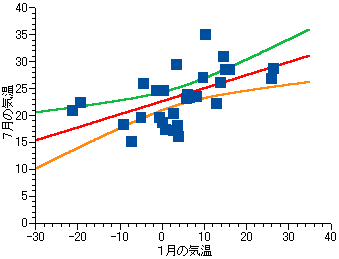
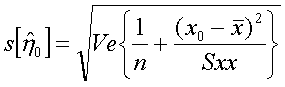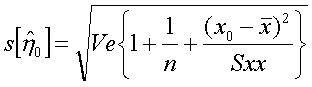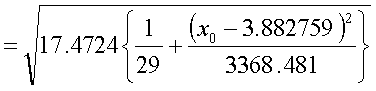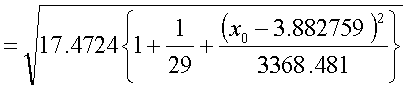エクセルを利用した回帰分析の手順
1.回帰分析を適用するのは本当はよくないのですが、宿題の例として用いましたので、北半球の1月の平均気温から7月の平均気温を説明する回帰式を求め、回帰分析することにしましょう。
2.エクセルで回帰分析した結果、下の表のような結果を得ました。
3.回帰式はしたがって、
7月の平均気温=22.42356+0.2426×(1月の平均気温)
となりました。
4.回帰係数の95%信頼区間は
0.094825〜0.390375 となりました。
回帰係数の検定はt値が3.368458なので、回帰を求めるために使用したデータ数が29から、自由度は27、t(27,
0.01)=2.771なので、1%水準で回帰係数は有意であることがわかりました。P−値をみても0.002287と0.01より小さいので同じことがいえます。
5.回帰分析による区間推定
1月の気温として5℃を与えたときに、7月の平均気温はどうなるかは、回帰式に代入すると求められます。
22.42356+0.2426×5=23.63656
計算結果から23.6℃となりました。
95%信頼区間を求めてみましょう。まず分散分析の結果から残差の分散をみつけます。17.4724とあります。これが誤差分散Veとなります。回帰を求めるのに使ったデータ数は29、誤差の自由度は29-2=27となります。Sxxはxの平方和です。xの平方和をパソコンで求めるにはxの分散にn-1=28をかけると求められます。以上からまず次のx0に対するyの信頼区間を求めるための標準誤差を次の式で求めます。
今回の回帰分析の結果を代入すると、
95%信頼区間を求めるにはこの値にt(n-2,0.05)=t(27,0.05)=2.052をかけます。
したがって、x0が5℃のときには95%信頼区間は
(23.6-0.780366×2.052, 23.6+0.780366×2.052)
=(22.0, 25.2)
となります。
6.回帰による区間予測
推定は母平均に関するものですから、上の場合、1月の気温が5℃である地点について7月の平均気温を調べると平均は22.0〜25.2℃に95%の確率で入ることを意味します。しかし、ある一地点の温度がどうなるかを知りたい場合には予測となり、信頼区間はもっと広い幅を持ちます。予測の場合には、x0に対するyの信頼区間を求めるための標準誤差を次の式で求めます。
今回の回帰分析の結果を代入すると、
95%信頼区間を求めるにはこの値にt(n-2,0.05)=t(27,0.05)=2.052をかけます。
したがって、x0が5℃のときには95%信頼区間は
(23.6-4.25222×2.052, 23.6+4.25222×2.052)
=(14.9, 32.4)
となります。
7.推定と予測の信頼区間をグラフにかくとそれぞれ下の図のようになります。推定(左)、予測(右)です。