第10回 分散分析その2 二元配置の分散分析
1.2つ以上の要因について,その効果を考えたい.
前回の授業では一元配置の分散分析について学びました.一元配置の分散分析では一つだけの要因について,その要因がデータの変動に関与しているかを,データの変動を要因によって変動した部分と偶然誤差による意味のない変動に分けることによって,解析しました.一元配置の分散分析では例えば,餌の種類が羊の成長に及ぼす影響があるのか,あるいは肥料の量が水稲の収量に及ぼす影響があるのかを検出できます.
今度は,2つ以上の要因について,それらの要因がデータの変動に関与しているかを解析します.例えば,餌の種類に加えて,品種の違いが羊の成長に及ぼす影響があるのか,あるいは肥料の量に加えて,作期の違いが水稲の収量に及ぼす影響があるのかを解析したいとします.
さて,先ほど述べた効率的に見えた実験は一事一時計画といいます.この古典的な方法は一方の要因Aを固定しておいて,もう一つの要因をb変化させ,変化させた要因のb最適な水準を決め,次に要因Bを固定して,今度は要因Aの最適な水準を決め,その結果の組み合わせを要因Aと要因Bの最適な組み合わせとしました.しかしこのやり方には次のような問題があります.
例:ヤギの成長がよくなる薬A,B,C,Dは餌と混ぜて使用する.混ぜる餌の種類によって薬の効果が異なるかもしれないので,麦わら,稲わら,濃厚飼料の3種類と組み合わせて試験したい.
この試験では要因(処理)は2つあり,薬と餌です.そして,薬は5水準(対照区を含める),餌は3水準あります.比較すべき試験は薬A+麦わら,薬A+稲わら,薬A+濃厚飼料,薬A+麦わら,薬A+稲わら,薬A+濃厚飼料,薬B+麦わら,薬B+稲わら,薬B+濃厚飼料,薬C+麦わら,薬C+稲わら,薬C+濃厚飼料,薬D+麦わら,薬D+稲わら,薬D+濃厚飼料,対照区+麦わら,対照区+稲わら,対照区+濃厚飼料となります.
古典的な試験法ではまず薬品で一番効果のあるもの(例えば薬C)を,固定した餌(例えば麦わら)で決定し,その後,薬Cを固定して,3つの餌のうちどれがよいかを決めます.しかし,もし麦わらでは薬Cが一番効果があったが,稲わらでは薬Bが最も効果が高かったとしたら,この方法では検出できません.このように2つの要因の絡み合った効果を交互作用といいます.
交互作用にはいくつかの種類があります.
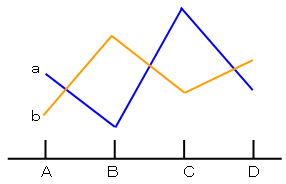
A.組み合わせの妙
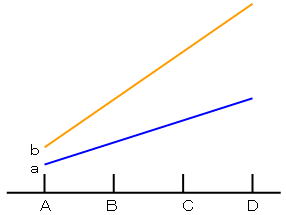
下の図のようにある特定の組み合わせだと反応が高くなる(あるいは低くなる)ということがおこる場合,交互作用があることになります.下の図ではもし始めにA,B,Dのどれかを固定して,aとbを比較したら一番最適な組み合わせであるCとbは発見できません.
B.相乗効果
2つの要因が重なるとより効果が大きくなる場合です.
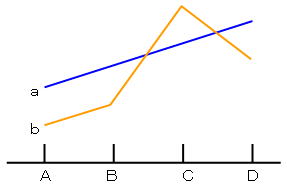
C.打ち消しあう場合(相殺効果ともいう)
片方の要因の効果が高いともう一方の要因の効果がうち消す場合です.
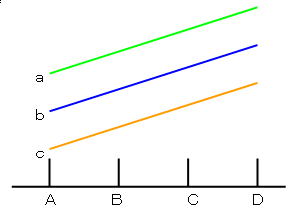
D.交互作用のない場合
右のような図になれば,交互作用はありません.しかし,こういうときでも2つの要因を同時に実験する方が,実験の効率がよく,誤差も小さいことがわかっています.
5.二元配置の分散分析
分散分析ではデータの変動(ばらつき)を偶然誤差による意味のないばらつき(誤差変動)と処理による変動にわけ,誤差変動に対して,処理による変動が十分に大きいかをF検定で検定する方法です.したがって,誤差変動をできるだけ小さくすることができれば,F検定での検出力が高まるはずです.
要因が2つあるときには,要因A,Bとすると
総変動=要因Aおよび要因Bによる変動+誤差変動
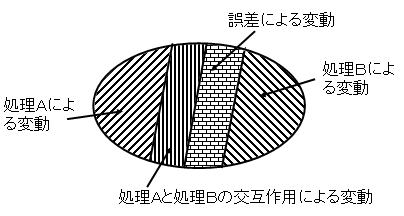
=要因Aによる変動+要因Bによる変動+要因Aと要因Bの交互作用による変動+誤差変動
以上のようにデータのばらつきを分離することができます.交互作用による変動を分離するには同じ処理の組み合わせについて2つ以上のデータの反復が必要になります.反復のないときは交互作用による変動と誤差変動を分離できません(交絡しているといいます).
6.宿題
A.先週の宿題3.で得たデータについて,以下のことを行いましょう.
1. 繰り返しのある二元配置の分散分析を行いましょう.
2. 交互作用については有意差があるなしに関わらず,各処理の反復間の平均値を使って,グラフを書き,どのような交互作用があるのか(相乗効果,組み合わせの妙など)を考えましょう.
3. さらに交互作用の大きさと主効果の大きさを比較し,検討しましょう.
B.実験計画法における基本的な考え方であるフィッシャーの三原則とは1.反復,2.無作為化,3.局所管理です.
局所管理の例として,5品種の水稲について収量を比較する実験を考えてみましょう.1つの品種について1反復について20m2の水田が必要であるとしましょう.3反復の実験を行うので,20×3×5で300m2の水田が必要となります.300m2の水田が地力ムラのない均一な水田であれば何の問題もありませんが,現実にはそのような水田はほとんど見つからないでしょう.こういうとき反復ごと,すなわち比較した5つの品種が1セット入る水田はなるべく均一になるようにして,100m2のブロックを3つ作ります.これが局所管理です.水田の中で,地力の高いところ,中くらいのところ,低いところの3つに分け,それぞれのブロック内では土を混ぜるなどの操作でムラをなるべく減らすようにします.
さて,このような局所管理は実験のいろいろな場面で要求されます.以下の実験では,どのような局所管理が必要かを考えてみましょう.
A.何人かのモニターに3種類のレトルトカレーの新製品を試食してもらう.
B.実験に未熟な3人が,5種類のトマトの酸度について,ビューレットで滴定する方法で調べた.
C.日当たりのあまりよくない谷間で5品種の柿の収量実験を行う.
3.交互作用のいろいろ
そこで,処理が2つになった場合,処理A,処理Bそれぞれについて
総変動=処理Aによる変動+処理Bによる変動+誤差変動
に分解できないか?と考えます.
そうすると誤差変動に対して,処理A,処理Bの変動をそれぞれF検定できるのではないでしょうか?
しかし,次のような意見もあるかもしれません.同時に処理Aと処理Bを実験しなくても,一つ一つやった方が確実ではないか?だいいち,次のように考えると,同時に2つの処理を実験するより,一つ一つやった方が確実な上に,効率的ではないか?・・・
2.要因計画と一時一事計画
例:おいしいパンを焼くオーブンの温度と焼く時間を決めたい.
因子X:オーブンの温度3段階,因子Y:焼く時間3段階,反復2回とします.
別々に実験すると
温度実験 3段階×2反復=6回の実験
時間実験 3段階×2反復=6回の実験
あわせて12回の実験
組み合わせた実験をする
温度3段階×時間3段階×2反復=18回の実験
さらに先ほどのおいしいパンを焼く実験では次のような問題が生じます.
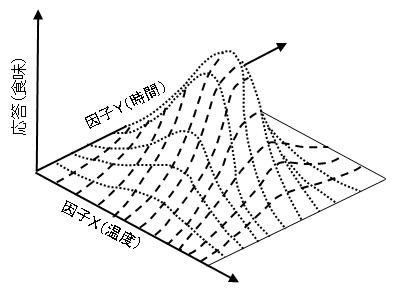
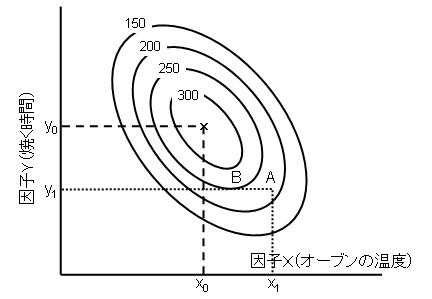
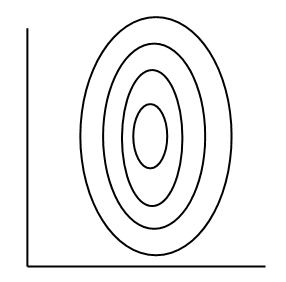
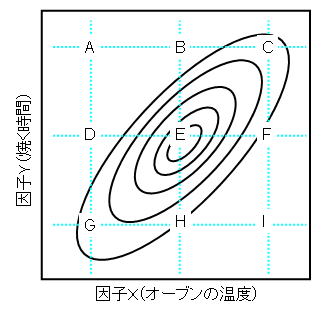
温度と焼く時間の2つの因子が組み合わさった応答である食味が下の左図のようになるとします.これを等高線グラフにしたものが下の右図です.
もし一時一事計画を採用すると,最初に例えば温度x1で実験したとしましょう.このとき焼く時間はy1が最適な時間となります.次に焼く時間をy1に固定して,焼く温度を変えると,点Bが最適な組み合わせということになります.でも実際にはまん中のX点が最適な条件の組み合わせです.このように一つ一つ要因を順番に実験していくと最適な条件にたどり着かないことがあります.これも2つの因子に交互作用があるからです.もし交互作用がない場合,等高線図は下のようになります.
このような交互作用による効果も考慮すると,できれば,総変動を次のように分解したいということになります..
総変動=処理Aによる変動+処理Bによる変動+処理Aと処理Bの交互作用による変動+誤差変動
そして,誤差変動に対して,処理Aによる変動,処理Bによる変動,処理Aと処理Bの交互作用による変動それぞれが有意に異なるのかを検定できないかと考えます..
4.要因計画 2つ以上の要因について同時に実験する実験計画法を要因計画といいます.
要因計画の利点は主に下の3つです.
1) 実験効率が高い
2) 交互作用を検出できる
3) 最適水準を検出できる
1) 実験効率が高い
別々に実験すると 2反復で,12個の実験で少なく実験がすみそうに見えます.
しかし,交互作用がなければ上の実験で温度について3反復,時間についても3反復の実験と考えられます.すなわち別々にやるより,反復数も多く,回数も少なくてすむので,実験効率が高いことになります.
組み合わせ実験では,交互作用がなければ下のように各組み合わせは反復をもうけなくてもよいことがわかっています.
2) 交互作用を検出できる
要因計画では,
総変動=処理Aによる変動+処理Bによる変動+処理Aと処理Bの交互作用による変動+誤差変動
に分解し,分散分析によって,交互作用を検出することができます.
3) 最適水準を検出できる
右の図のように因子Xについて3水準,因子Yについて3水準の実験を組み合わせて,合計A〜Iまでの9つの実験を行うと,最適水準にほぼ近いE点を検出できます.