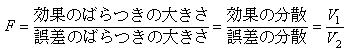一元配置の分散分析ではどのようにして処理の効果と誤差によるばらつきを分離したのか？

一元配置の分散分析では
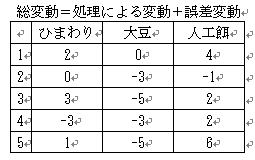
　総変動＝処理による変動（主効果）＋誤差変動
　に分解することができました．

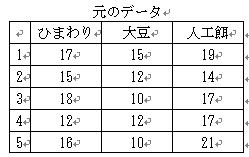
例：ハムスターをひまわり，大豆，人工餌の３種類のどれで育てるのが一番よいかを実験した．

１．実験の結果，右のようなデータが得られたとします．

２．データの変動は全体の平均からのずれと考えられます．平均は15なので，元のデータから15を引いたものが総変動になります．
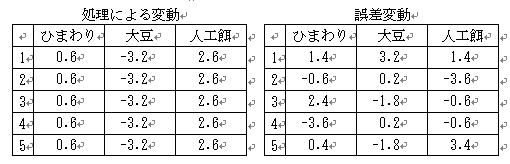
　この総変動は処理による変動と誤差変動に分けることができます．

３．処理による変動が誤差による変動に比べて，十分に大きいのか（正確には処理による変動と誤差による変動は等しいという帰無仮説が棄却できるのか）をＦ検定で検討します．
帰無仮説：　効果による変動と誤差による変動には差がない．
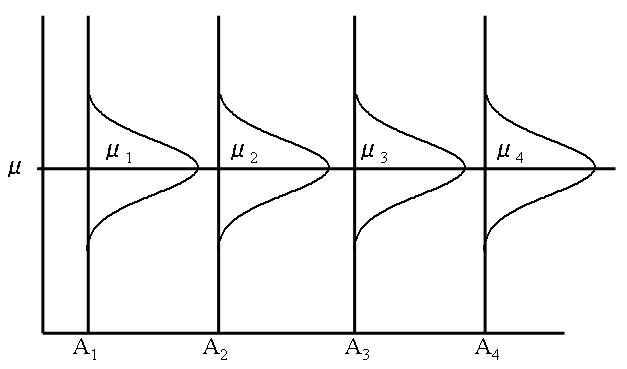
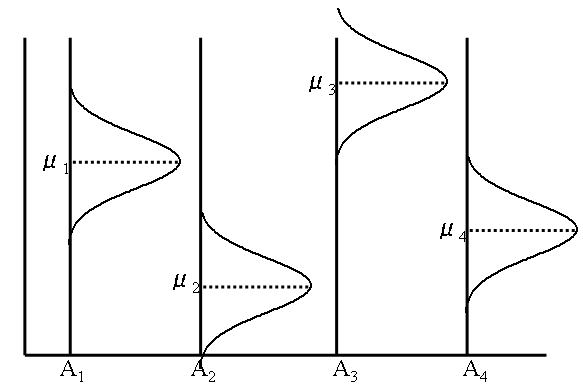
上の帰無仮説のいうことは下の図のように読み替えることもできる

帰無仮説：μ_１＝μ_２＝μ_３＝μ_４　どの水準でも母平均は同じである（左下図）
対立仮説：水準（処理）間の母平均のどれか一つは異なる（右下図）

　次の分散比Ｆを計算し，この分散比が得られる確率Ｐ値を計算します（実際はエクセルなどのソフトがデータを入力しただけでＰ値を計算する）