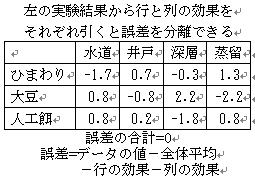
二元配置の分散分析の仕組み（どうやって，処理の効果と誤差を分離するか？）

例：ハムスターをひまわり，大豆，人工餌の３種類と水道水，井戸水，海洋深層水，蒸留水の４つの水のどれで育てるのがいちばんよいかを実験した．
以下の解析は「実験計画と分散分析のはなし」大村平著日科技連を参考にしました．

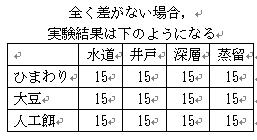
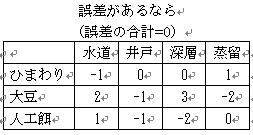
１．餌の効果も，水の効果も，誤差も何もないときは，右のような結果になるはずです．要するに全部同じ値をとります．

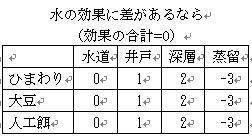
２．もし水の違いによってハムスターの成長が変わるとしたら，例えば右のような効果があれば，

２つを合計して，右のような実験結果が得られます．

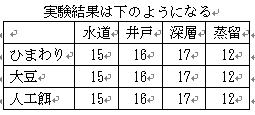
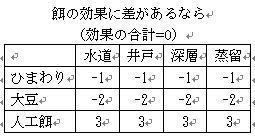
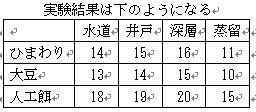
３．さらに餌の違いによってハムスターの成長が変わるとしたら，例えば右のような効果があれば，

２つを合計して，右のような実験結果が得られます．

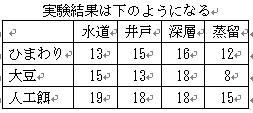
３．このような実験結果に右のような誤差がつきまとっていたとします．

結局，水の効果，餌の効果，誤差の３つを合わせた結果は右のようになります．

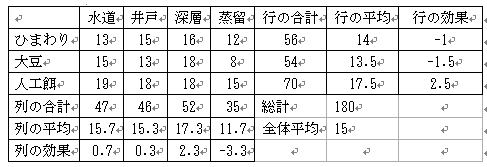
４．次にこのようにして得られた実験結果から餌の効果，水の効果を分離します．

５．誤差を分離します．誤差=データの値−全体平均−行の効果−列の効果から計算できます．

６．したがって，ここでは総変動＝土の効果＋餌の効果＋誤差変動（繰り返しがないと交互作用は検出できません）と分解できました．

７．誤差変動に比べて，水の効果や餌の効果が大きいかどうかはF検定で判定します．

８．以上の実験では各処理に反復がないので，交互作用を検出できませんでした．交互作用はどうやって検出するのでしょうか？

　いつものハムスターの例から　２水準の処理を２つ組み合わせて，それぞれの処理の組み合わせについて２反復実験しました．その結果，下のようになりました．．

　餌の因子変動は大豆対人工餌のばらつきであるから，餌と土の交互作用では，
大豆で水道水，人工餌で井戸水　　　対　　　大豆で井戸水，人工餌で水道水

　このように比較すると大豆のときは水道水がよく，人工餌のときは井戸水がよいというような交互作用が強ければ強いほど，この対立は顕著に現れることになります．

　上の数字が青地の部分と黄色地の部分とを対比させて，交互作用による変動を求めます．全体の平均は15ですから，

　青地の部分（大豆で水道水，人工餌で井戸水）では
　合計＝17+20+12+14＝63
　平均＝合計÷4＝15.75
　交互作用の効果＝平均−15＝0.75

　斜字体でない部分（大豆で井戸水，人工餌で水道水）では
　合計＝24+9+17+7＝57
　平均＝合計÷4＝14.25
　交互作用の効果＝平均−15＝-0.75

以上のようにして，実験結果から交互作用を分離することができます．実際の計算ではこのやり方ではあまりにも面倒なので別の方法を使います．なお今ではパソコンがデータを打ち込めば計算するので，交互作用の計算に苦労するのは過去の話になりましたが．

実際に繰り返しのある二元配置から交互作用を計算する方法を以下で説明します．ちょっと複雑なうえに，説明も要領をえないですが，これがわかれば，どんな分散分析も原理からその気になれば（大変な作業だけど，エクセルを使えばなんとかなりそうですね）計算できるでしょう．さらに分散分析の仕組みもよく理解できるようになると思います．時間のある人は自分でいろんなパターンをつくってみて，分散分析をしてみては？