正規分布の特徴を具体的に考えてみましょう.20~24歳の男性の身長は人間生活工学研究センターの調査(1992-1994)によると,平均(μ)170.5cm,標準偏差(σ)5.9cmでした.身長の分布が正規分布に従うとしますと,このことから2σ以上平均より背の高い人,すなわち182.3cm以上の人は全体の2.2%になります.平均から標準偏差以内,すなわち164.6~176.4cmに全体の68%が属します.全体の95%は158.9~182.1cmに属します.
1.正規分布
正規分布は自然界で起こる現象の多くがその分布に当てはまること,特に平均値に関する分布が当てはまることから,統計学では最も重要な分布となっています.
この結果から,どのような母集団であっても,標本平均の分布については以下のことがいえそうです.
1) 標本平均の分布の平均は母集団の平均とほぼ同じになることが多い.
2) 標本平均の分布は正規分布に近い形をしている.
3.標本平均の分布
私たちが母集団について何らかの性質を知りたいために,その中から無作為に標本を抽出します.たいていまず第一に知りたいことは母集団の平均(母平均)です.では標本の平均と母集団の平均にはどのような関係があるのでしょうか?
以上の結果を利用すると,マッチの火が10 秒以内に消える割合は,10 を対数変換し,2.30 を得ます.ここからその割合は84%であると計算できます.
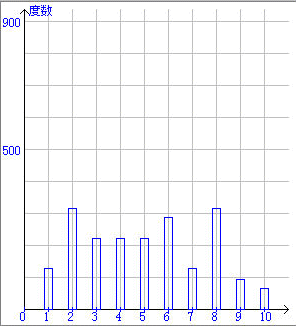
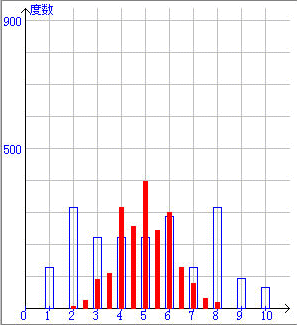
上左の図が母集団の分布を示します.この母集団から5つの標本を無作為に抽出し,その平均をとります.この試行を2000回繰り返し,得られた標本の平均の分布を示したのが,上右の図です.
それではまず,正規分布の特徴を以下に列記します.
平均μ,分散σ2の正規分布はN(μ,σ2)と表記され,以下のことがいえます.
さて,標本を取る数を5個よりも多くすると,標本平均の分布はどうなるでしょうか?同じようにシミュレーションしてみました.
ある母集団について,標本を5つ無作為に抽出するという試行を2000回繰り返してみました.
下がその一例です.なおこのシミュレーションは講談社ブルーバックスB-1403
パソコンで遊ぶ数学実験 涌井良幸・涌井貞美著についているCD-ROMのプログラム(No.14)によって行いました.
2.正規分布への変換
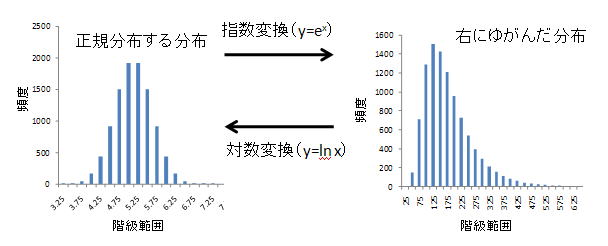
母集団が正規分布しない場合でも,数値を変換することによって正規分布に近似できることがよくあります.正規分布する分布について,その個々の数値を指数変換(y=ex)すると右にゆがんだ分布を得ることができます.このような右にゆがんだ分布は年収,貯蓄などの分布にみられます.したがって,年収のように右にゆがんだ分布では,対数変換してやることによって,正規分布に近似できることがあります.
下の図は第1回の授業で使ったA池の魚の体重の分布を使って,数値変換を行ったものです.A池の魚の体重は正規分布するので,個々の値を指数変換し,ヒストグラムをとると右の図のように右に(正に)ゆがんだ分布になります.逆に考えれば,右にゆがんだ分布は対数変換すれば正規分布に近似できそうだといえます.
エクセルにおける正規分布の計算の詳細は以下をクリックしてください.
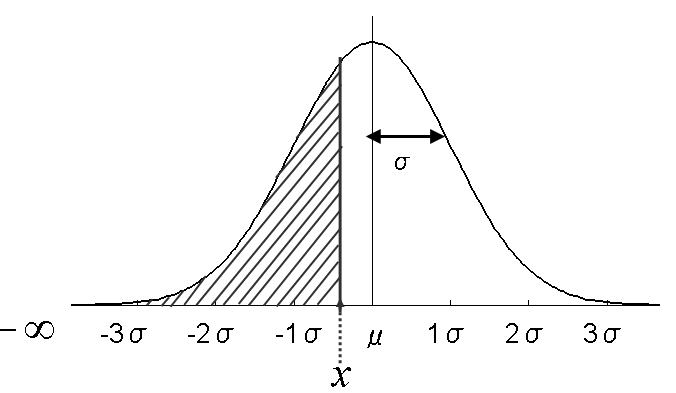
- 平均μを中心にして,左右対称である.すなわち平均とメジアンは一致する.そして,平均より大きい値あるいは小さい値を取る確率はどちらも1/2である.
- 曲線は平均μの近傍で高く,両側に行くにしたがって単調に低くなる.
- 平均μは曲線の位置を決める.平均μのみ異なる2つの曲線は左右に移動させれば重ねることができる.(参考図)
- 標準偏差σは曲線の形を決める.σが大きければ曲線は扁平になる.(参考図)
- μ-σとμ+σの間の確率変数を取る確率は約0.68である.(参考図)
- μ-2σとμ+2σの間の確率変数を取る確率は約0.95である.(参考図)
- μ-3σとμ+3σの間の確率変数を取る確率は約0.997である.(参考図)
- 0.95(95%)の確率でμ-1.96σとμ+1.96σの間の確率変数をとる.(参考図)
- 0.99(99%)の確率でμ-2.576σとμ+2.576σの間の確率変数をとる.
この結果から,どのような母集団であっても,標本平均の分布については以下のことがいえそうです.
3) 標本の数を増やすと標本平均の分布のばらつきが小さくなる.
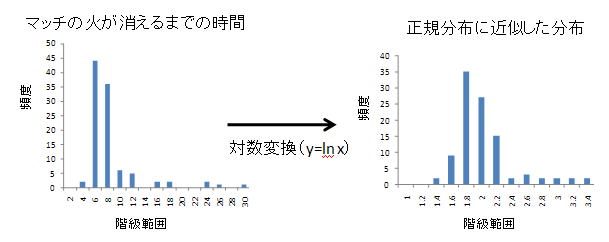
例:マッチの火が消えるまでの時間を測定した結果のヒストグラム(左)であり,ここから対数変換すると正規分布に近似できそうであると考えました.各測定値を対数変換した結果,右下のヒストグラムを得ました.ほぼ正規分布しているとみなして,この対数変換後の値について平均,標準偏差を計算したところ,平均=1.92,標準偏差=0.39
となりました.
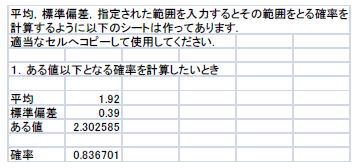
平均がμ,標準偏差がσである正規分布において,x以下の範囲に属する割合を
NORMDIST(x, μ, σ, true)で計算します.下の図の斜線の割合を求める関数です.
正規分布はかなり難しい数式で表現されます.しかし,エクセルでは正規分布に関する関数がいくつかあるので,数式を知らなくても正規分布に関する計算を,エクセルを使って,することができます.
さて,標本平均の分布は母集団の分布の形に依存するでしょうか?いろいろな母集団について同じ実験をしたら,次のような結果を得ました.