- 本日の作業内容
- 前回の復習
- 解析的に解けない場合の計算を数値計算を用いて行う
- 物理モデルに基づいて複雑で膨大な計算を行う
- 乱数を用いてランダムな挙動を取り込んだ計算を行う
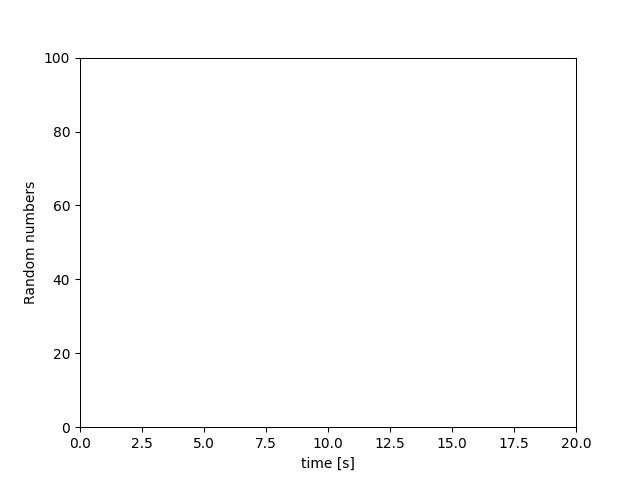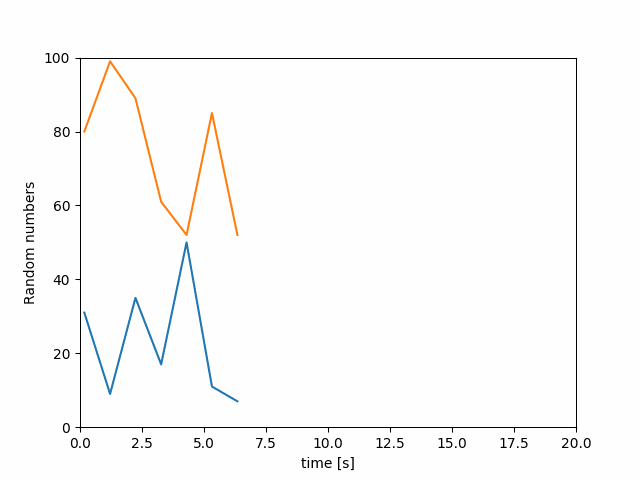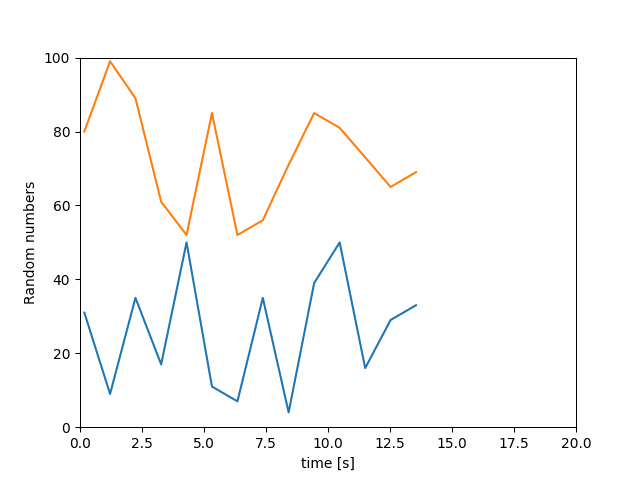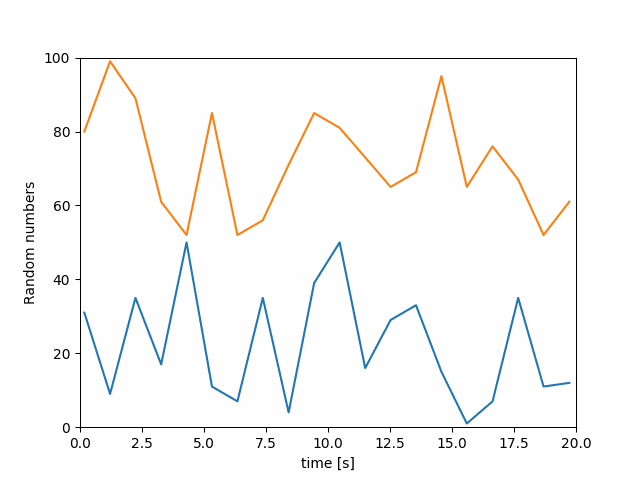
- 再描画
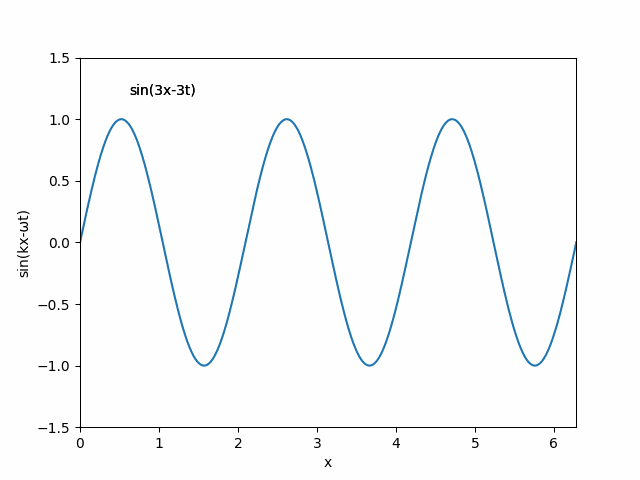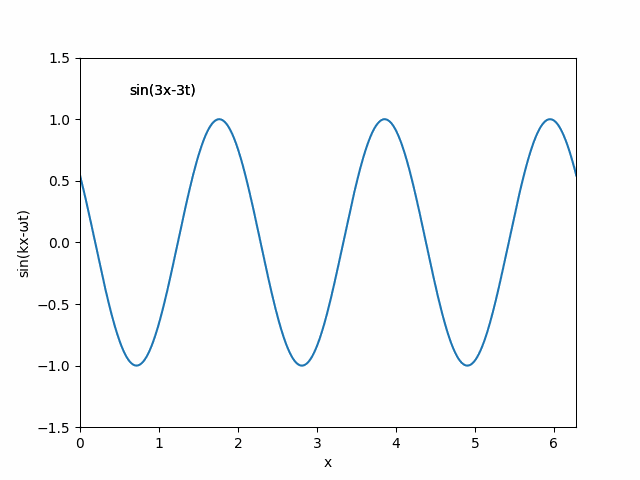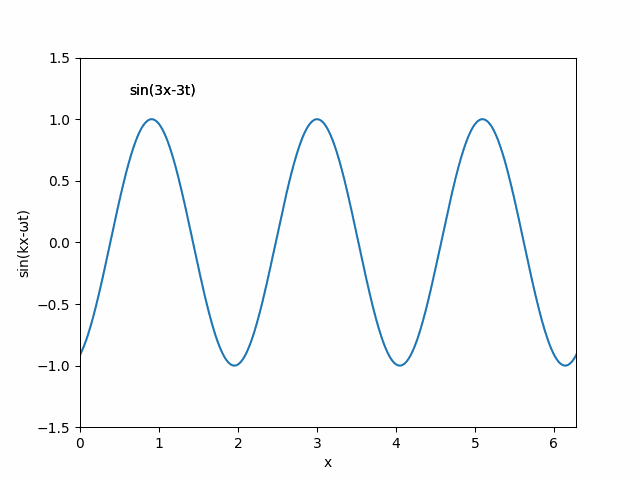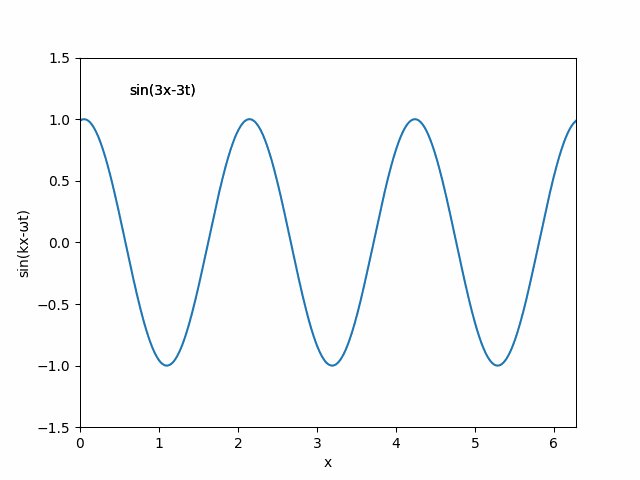
- 進行する平面波
今回は解答用紙に番号と名前の無いものが出てきてしまいました.注意しましょう.
num and name: 24_57
以下は例によって問題のあるものなのですが,今回はグラフのプロットなので,結果の図でお示しします.

今回一番多かったものが上の例で,tight_layout() を指定しなかったために右Y軸のキャプションが切れているものでした.
次に多かったのは凡例の不適切な表示で,以下のようないろんなパターンが見られました.


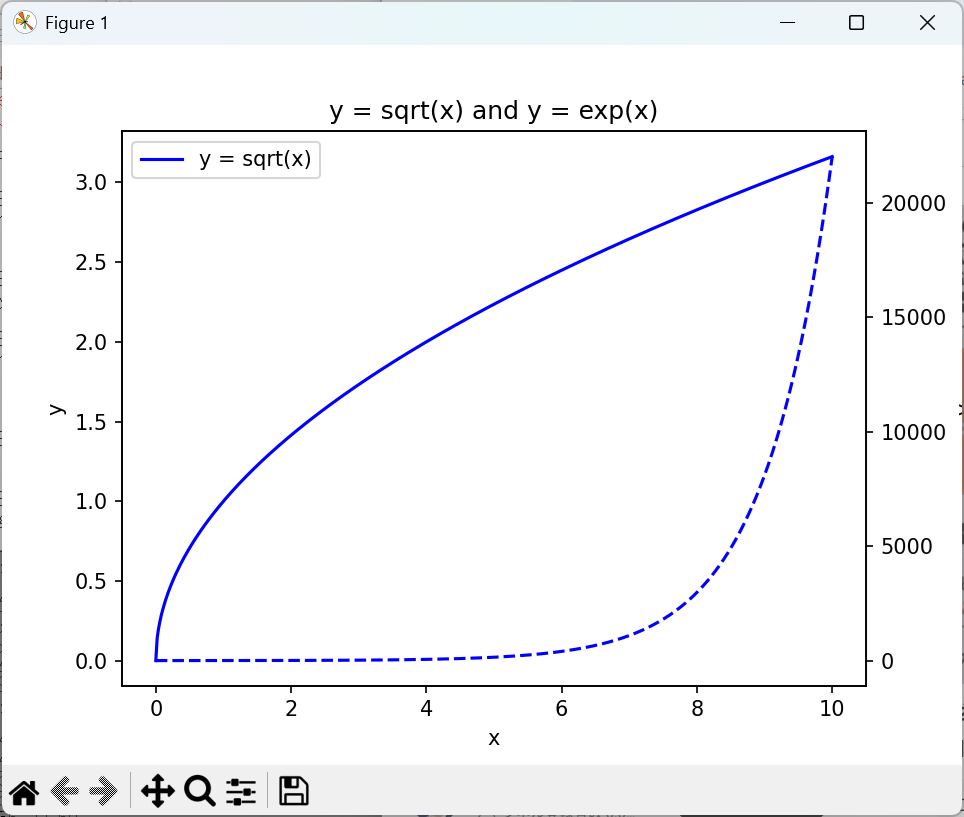
一番残念なのは以下のもので,今回の主題であるダブルY軸になっていないもので,さすがにこれはダメですね.
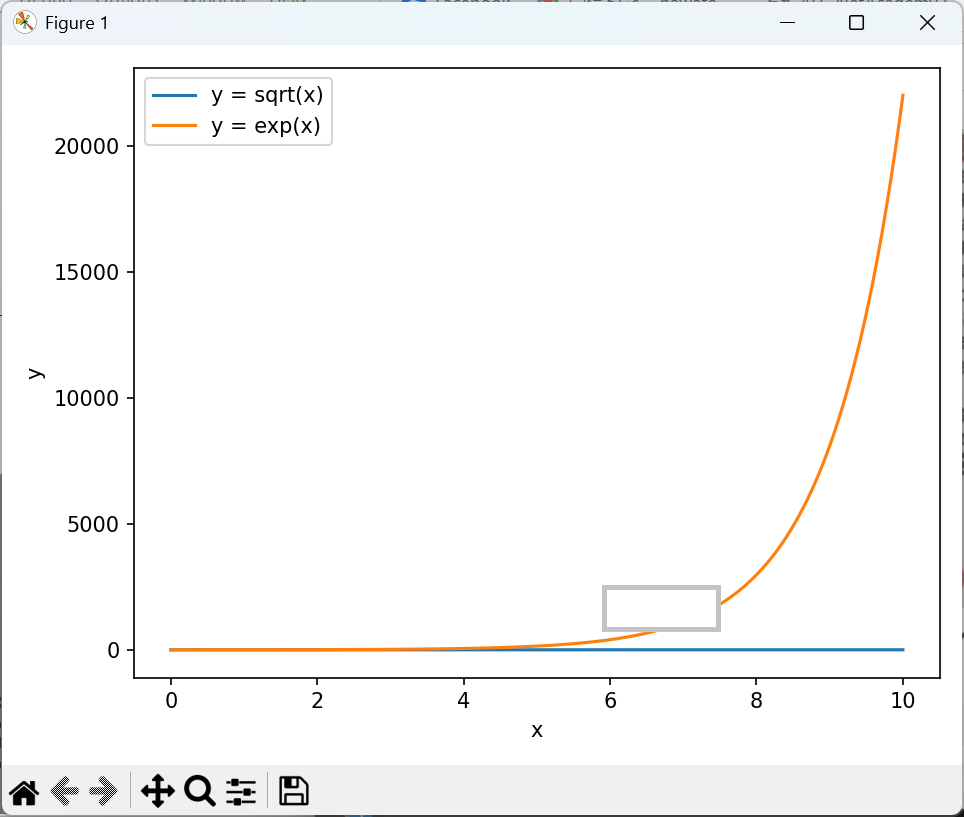
Wikipedia によりますと,シミュレーションとはラテン語の similis (似ている),simulare (模倣する),simulat (真似た)などの言葉から生まれた概念とされています.対象となるシステムで働いている法則を推定・抽出し,それを真似るようにして組み込んだモデル,模型,コンピュータプログラムなどを用いて行われます.現実のシステムを動かしてその挙動や結果を確かめることが困難,不可能または危険である場合に用いられるものとされます.
昨年NHK朝ドラ「虎に翼」で話題になった戦前の日本の「総力戦研究所」が行った模擬戦では日本がアメリカに必ず負けるという結果になったことは有名ですね.
「シュミレーション」と言われることも多いようですがそれは音位転換であり,「シミュレ」よりも「シュミレ」の方が日本人には発音しやすいことに起因します.
シミュレーションをコンピュータを用いて行う場合にコンピュータシミュレーションと呼ばれます.
今回は乱数を用いて実際に実験可能な作業を数値化して画面に動画で実行結果を表示することにします.
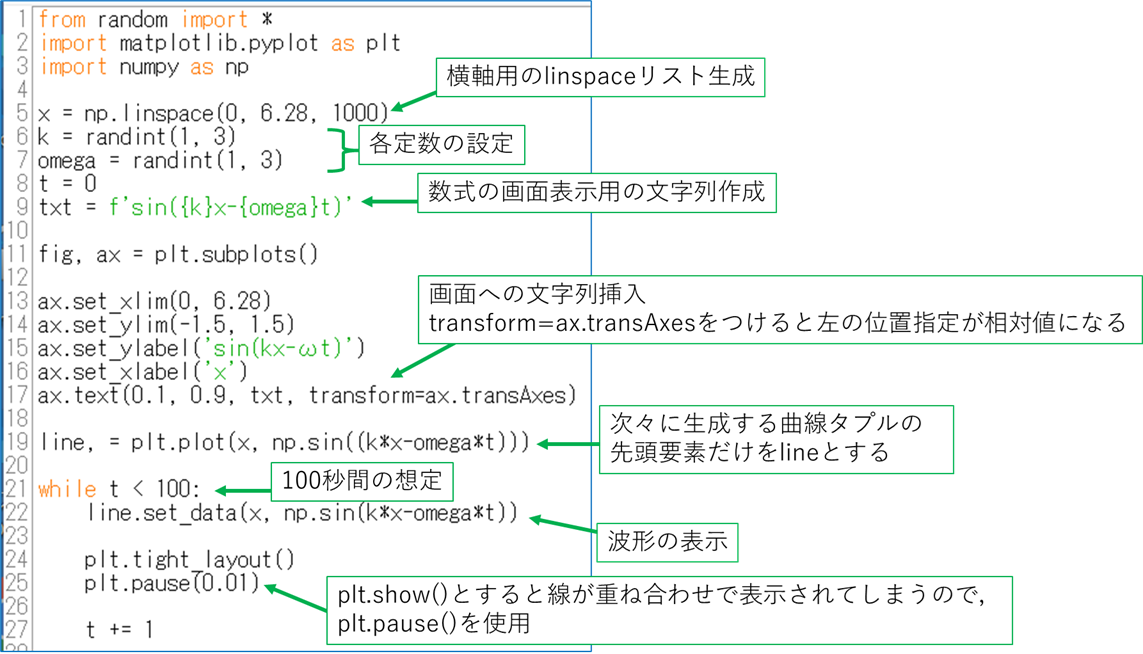
シミュレーションの状況を動的に提示するために,グラフを逐次再描画する方法が使えます.以下では,それを試してみましょう.
ご存じのように1次元の進行波は以下の式で表現されます.
f (x, t) = sin(kx - ωt)
ここで,k は波数,x は座標,ω は各振動数,そして t は時間です.乱数を用いて,k を1から3の定数,ω も同じく1-3の整数として,進行波を表示する動画を作製します.以下のソースをご覧ください.
from random import *
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 12, 1000)
k = randint(1, 3)
omega = randint(1, 3)
t = 0
txt = f'sin({k}x-{omega}t)'
fig, ax = plt.subplots()
ax.set_xlim(0, 12)
ax.set_ylabel('sin(kx-ωt)')
ax.set_xlabel('x')
ax.text(0, 0.9, txt, transform=ax.transAxes)
line, = plt.plot(x, np.sin((k*x-omega*t)))
while t < 100:
line.set_data(x, np.sin(k*x-omega*t))
plt.tight_layout()
plt.pause(0.01)
t += 1
|