先週の演習問題の ii. および iii.を使用して,結果をグラフで表示するプログラムを作成しましょう.特にモジュールにしたり,CSVデータの保存・読み込みをしなくても良いので,データを作製して,近似直線を求め,プロット点とともに表示させましょう.
x y 0.881 1.585 1.925 4.124 2.933 6.318 4.056 8.143 4.906 9.827 6.065 12.440 7.017 13.231 7.921 16.318 8.862 18.406 9.945 18.960 Fitted line: y = 0.236 + 1.963 x |
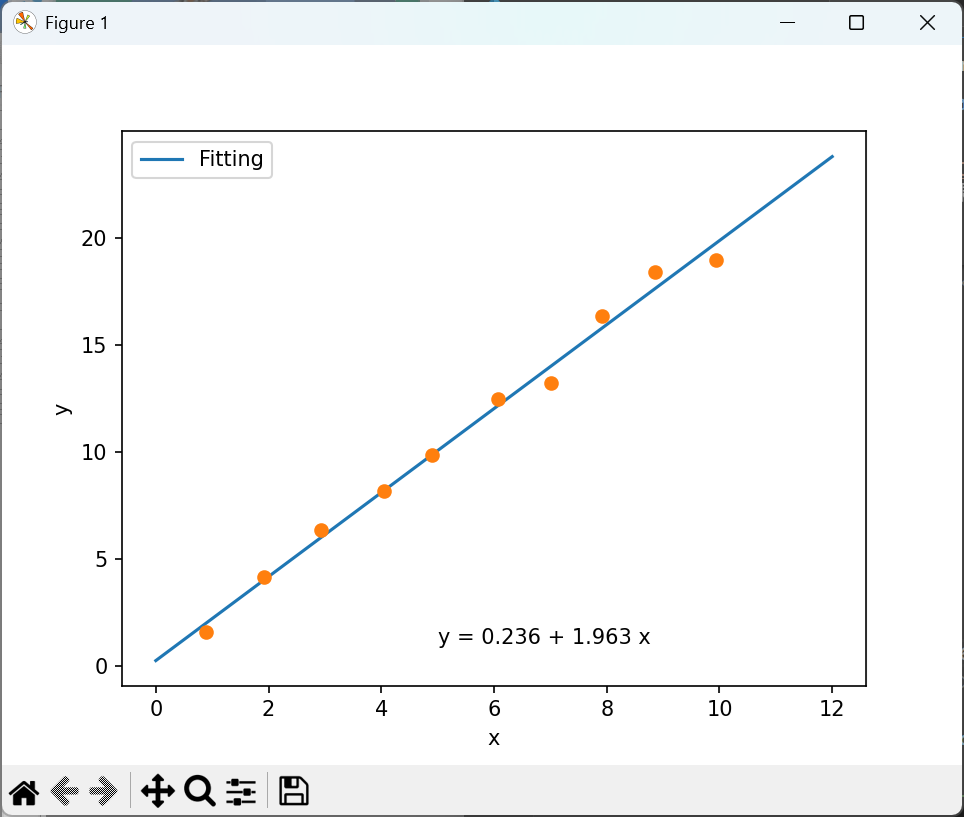
ついでに数式もグラフ内に入れました.以下のようにしています.
5, 1 は表示位置で x が5で y が1の場所を意味します.eq というのは数式の文字列です.
近年日本の少子化が大きな問題となっていますが,都道府県別の合計特殊出生率の最新版を用いて,国内の状況を見てみましょう.
都道府県別の出生率に各都道府県の県庁所在地の緯度と経度をつけたものを用意しました.緯度と経度は通常度分秒の角度単位で表示されていますが,それらの記号 ˚ ' " はプログラムの処理に影響を及ぼしてしまうので,ここではハイフンで切れ目を入れています.
まずは,このデータを読み込んで,緯度と経度の分と秒の部分を10進小数に直して扱いやすいデータに変換しておきましょう.
| [['Prefecture', 'North', 'East', 'Birth rate'], ['Hokkaido', 43.06194444444444, 141.35444444444443, 1.01], ['Aomori', 40.82277777777778, 140.74694444444444, 1.14], ['Iwate', 39.70194444444445, 141.15444444444444, 1.09], ['Miyagi', 38.26833333333333, 140.86944444444444, 1.0], ['Akita', 39.72, 140.1025, 1.04], ['Yamagata', 38.25555555555555, 140.33972222222224, 1.17], ['Fukushima', 34.76083333333333, 140.47472222222223, 1.15], ['Ibaraki', 36.365833333333335, 140.4713888888889, 1.16], ['Tochigi', 36.555, 139.88250000000002, 1.15], ['Gunma', 36.38944444444444, 139.06333333333333, 1.2], ['Saitama', 35.86138888888889, 139.64555555555555, 1.09], ['Chiba', 35.60722222222223, 140.1063888888889, 1.09], ['Tokyou', 35.693888888888885, 139.70333333333332, 0.96], ['Kanagawa', 35.45027777777778, 139.63416666666666, 1.08], ['Niigata', 37.91611111111111, 139.0363888888889, 1.14], ['Toyama', 36.69583333333333, 137.2136111111111, 1.29], ['Isihikawa', 36.56111111111111, 136.6563888888889, 1.23], ['Fukui', 36.064166666666665, 136.20277777777775, 1.46], ['Yamanashi', 35.66222222222222, 138.56833333333333, 1.26], ['Nagano', 36.64861111111111, 138.19472222222223, 1.3], ['Gifu', 35.42638888888889, 136.75944444444445, 1.27], ['Shizuoka', 34.97555555555556, 138.38250000000002, 1.19], ['Aichi', 35.18138888888889, 136.9063888888889, 1.22], ['Mie', 34.718333333333334, 136.50583333333333, 1.24], ['Shiga', 35.01777777777777, 135.85472222222222, 1.32], ['Kyoto', 35.01166666666666, 135.76805555555558, 1.05], ['Osaka', 34.693888888888885, 135.50222222222223, 1.14], ['Hyogo', 34.69027777777777, 135.19555555555556, 1.23], ['Nara', 34.684999999999995, 135.80472222222224, 1.19], ['Wakayama', 34.23027777777778, 135.17083333333332, 1.24], ['Tottori', 35.49444444444445, 134.2188888888889, 1.43], ['Shimane', 35.46805555555556, 133.04861111111111, 1.43], ['Okayama', 34.655, 133.91944444444442, 1.27], ['Hiroshima', 34.39138888888889, 132.45194444444442, 1.29], ['Yamaguchi', 34.17805555555555, 131.4738888888889, 1.36], ['Tokushima', 34.07027777777778, 134.555, 1.32], ['Kagawa', 34.34277777777778, 134.04666666666665, 1.36], ['Ehime', 35.83916666666667, 132.76555555555555, 1.28], ['Kochi', 33.55888888888889, 133.53111111111113, 1.25], ['Fukuoka', 33.59, 130.40166666666667, 1.22], ['Saga', 33.26361111111111, 130.30083333333334, 1.41], ['Nagasaki', 32.74944444444444, 129.87972222222223, 1.39], ['Kumamoto', 32.80305555555555, 130.70777777777778, 1.39], ['Oita', 33.239444444444445, 131.60944444444445, 1.37], ['Miyazaki', 31.907777777777778, 131.42027777777776, 1.43], ['Kagoshima', 31.596944444444443, 130.55722222222224, 1.38], ['Okinawa', 26.21222222222222, 127.67916666666667, 1.54]] |
教科書 p.150 にある split を用いて - 区切りの文字列をリストに展開し, float に変換した後計算しています.
合計特殊出生率が都道府県の地図上の位置と関係があるのか,緯度の場合と経度の場合についてグラフにして確認してみましょう.
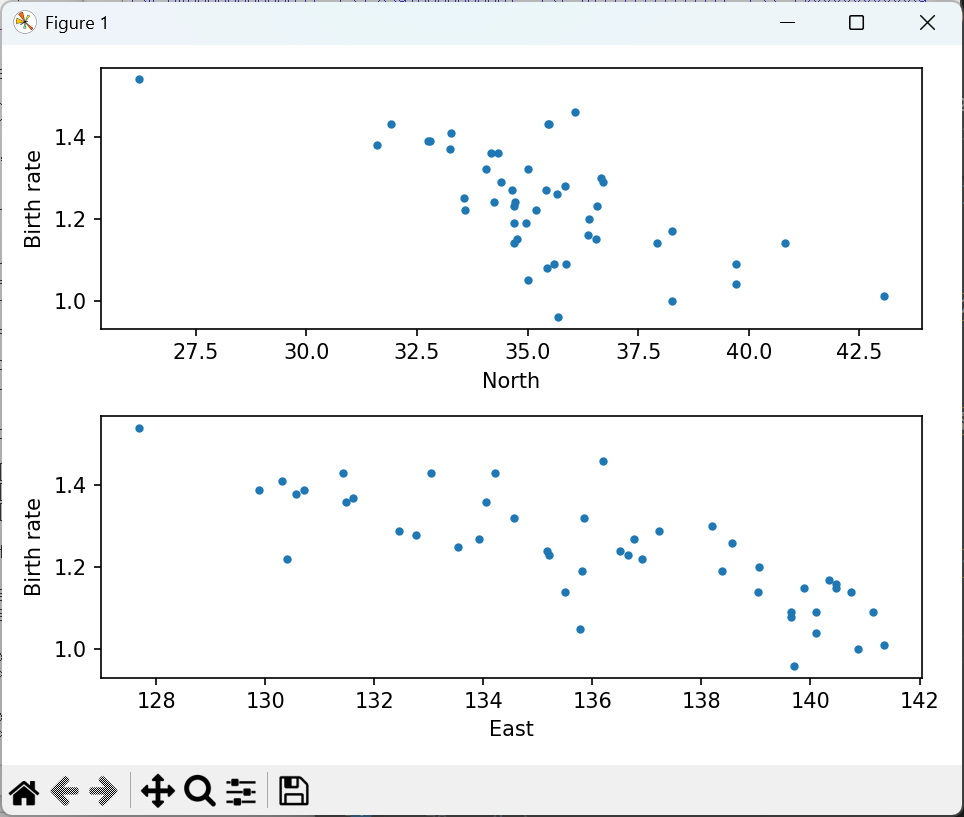
2つのグラフを表示する方法ですが,以下のように解答例では指定しました.
fig = plt.figure() ax1 = fig.add_subplot(2, 1, 1) ax2 = fig.add_subplot(2, 1, 2) ax1.set_ylabel(txtdata[0][3]) ax1.set_xlabel('North') ax2.set_ylabel(txtdata[0][3]) ax2.set_xlabel('East') ax1.plot(no, birth, '.') ax2.plot(ea, birth, '.') fig.tight_layout() plt.show()
subplot で指定している部分ですが,数字の1つ目が行数,2つ目は列数,3つ目が順番です.
numpy には相関係数を求める関数 corrcoef が用意されています.それを用いて,出生率と緯度,出生率と経度の相関係数を求めてみましょう.corrcoef は引数に2つのリストを与えると計算してくれます.
r = np.corrcoef(x, y)[0, 1] |
Correlation coefficients Latidue - birth rate: -0.*** Longitude - birth rate: -0.*** |
日本列島の形は東に行くほど北緯が上がるようになっています.ということは,県庁所在地の北緯と東経にはそれ自体相関があると思われます.そこで,前問で求めた緯度と出生率,経度と出生率の相関には,陰で緯度と経度の相関が影響していることが推測されます.
そのような隠れた相関の影響を取り除いて改めて相関係数を求めることが行われますが,その際の計数を偏相関係数と言います.以下の式で表されます.
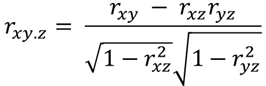
ここで,rxy.z は変数 z の影響を取り除いた x と y の間の偏相関係数で,上の式のように相関係数 rxy, ryz そして rxz から求められます.
では,実際に県庁所在地の緯度と経度の相関を取り除いた,緯度と出生率,経度と出生率の間の偏相関係数を求めて,日本の出生数の地理的要因についてより詳しく理解しましょう.
Partial correlation coefficients Latidue - birth rate: -0.*** Longitude - birth rate: -0.*** |