ｔ検定では２つの標本について，その母平均が異なるのかを検定しました．これを拡張して，３つ以上の標本についてその母平均が異なるのかを検定することを考えてみましょう．

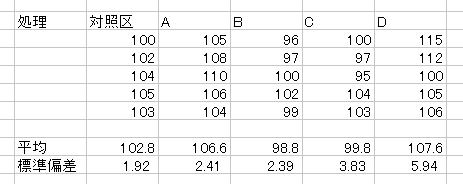
例：ヤギの成長がよくなるという薬Ａ，Ｂ，Ｃ，Ｄを対照区とともに調査した．薬剤処理は効果があるのかを知りたい．

上の例では，Ｄ＞Ａ＞対照区＞Ｃ＞Ｂの順で薬の効果が認められているようです．さて，ＡよりもＤが効果があるといえるかをｔ検定で検定し，さらに対照区よりもＡが効果があるといえるかをｔ検定し，これを何回も繰り返してよいのでしょうか．

ｔ検定はある特定の２つの標本についてある有意水準（例えば５％）で，その母平均に有意な差があるのかを検定します．しかし，それを繰り返すとデータ全体では５％以上の確率で誤った結論を下す可能性があります．

次の例を見てみましょう．これは1000羽のうずらの体重のデータ（平均，分散が同じ同一の母集団のもの）からランダムに10羽を選び，これを20回繰り返したものです．同一の母集団からでも20回も繰り返してデータを取ると，もっとも大きい値と小さい値の標本の間では有意差が検出されてしまうこともあります．すなわちヤギの薬の例でも20以上の薬を同時に実験したら，薬の効果がなくてもｔ検定では効果があるという結果が出てしまう危険があります．

ウズラの例では同じ母集団からでも何回も標本を取り出せば，その両極端の間にｔ検定で有意な差を検出することを示しています．したがって，このウズラについて何種類もの薬品について体重に変化があるのかを実験すれば，たとえ全くどの薬品にも効果がなく，母集団に変化がなくても，両極端を選ぶと差があると判断してしまいます．

この問題を解決する手法が分散分析です．名前は分散分析と分散の言葉がありますが，３つ以上の標本の母集団の平均に差があるかを検定する手段です．平均の差を検定するために分散を分析するとはどういう事なのでしょうか．

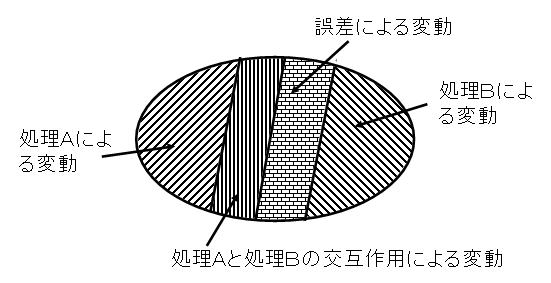
先ほどのウズラのデータをみるように，データにはもともとばらつき（誤差変動）があります．この誤差によるばらつきを，処理によって変化した値と混同してしまうことに問題があります．分散分析とはデータのうち，意味のない変動（誤差変動）と意味のある変動（処理によって変化した部分）に分けることによって，処理による変動が誤差に比べて十分に大きければ処理による変動があると判定する方法です．

２．前回の宿題３．で調べたデータについて分散分析せよ．

３．次回の授業では二元配置の分散分析について学ぶ．２つの処理を組み合わせたときのデータの解析方法である．
Ａ．産地と品種の違いがリンゴの糖度に及ぼす影響を知りたい．
Ｂ．施肥量と品種の違いがイネの1穂穎花数に及ぼす影響を知りたい．
Ｃ．作期と品種の違いがトマトの酸度に及ぼす影響を知りたい．
　二元配置で分散分析できそうなデータを研究室の卒業実験などから手に入れる．あるいは自分で実験してもかまわない．データには反復が２つ以上あること．データの配置は下の図のようになる．

産地と品種の違いがリンゴの糖度に及ぼす影響を各処理３つずつのリンゴで調査した．
産地　青森，長野，山形
品種　紅玉，ふじ，むつ

宿題
１．第５回の宿題で調査したデータを用いて，卵の重さのばらつきが２つ店の間で同じであるかを有意水準５％でＦ検定（両側検定）せよ．

それ以外にも次のような例が考えられます．
コンビニ弁当の売れ行き　曜日，天気の２つの要因
イネの1穂穎花数　品種，施肥の２つの要因
小鳥のさえずる回数　気温，太陽の明るさの２つの要因

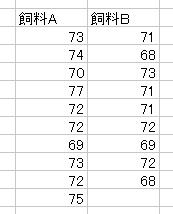
Ｐ値が0.25なので，帰無仮説は棄却できません．
したがって，５％の有意水準では飼料のばらつきに差があるとはいえないと結論できます．

例：Ａ，Ｂ２種類の飼料を与えて一定期間飼育したハムスターの体重の増加量を測定した結果，次のような結果を得た．飼料による体重増加量のばらつきに差があるのかを検定せよ．

Ｆ分布を利用して２つの標本の分散比を区間推定することもできますが，授業では省略しました．
Ｆ分布を利用した２つの標本の分散に差があるのかを検定できます．この手法はこれから学ぶ分散分析の基礎となります．

Ｆ分布は正規分布する母集団から無作為抽出された２つの標本の分散の比に関する分布を示します．２つの標本それぞれの自由度からＦ分布が決まります．次回の授業から学ぶ分散分析ではＦ分布を利用するので，大切な分布です．なかなか意味をとらえにくい分布かもしれません．

　さてどのようにしてデータの変動を誤差とそれ以外の処理による部分に分けるのでしょうか？

それは以下のページを見てください．

　分散分析は上のページで説明したようにデータの変動を解析するのですが，実際にそんなことを計算していたら大変です．昔はもう少しスマートな計算方法ではありながらも大変面倒な計算をしていました．とくに自由度はわかりにくい概念でした．しかし，今はパソコンでやれば，もともとのデータを入力してやるだけで分散分析できます．ここではエクセルの分析ツールによる分散分析の仕方を紹介します．

５．分散分析の注意点

５．　フィッシャーの３原則を満たした実験計画のもとで，分散分析を行います
　誤差に系統誤差が入ると解析結果の妥当性が失われる危険性があります．系統誤差を除去したり，分散分析の解析の妨害とならない偶然誤差に転化するのがフィッシャーの３原則に述べられた反復，無作為化，局所管理です．詳細は後の授業で学ぶ予定です．

１．　なるべく反復数はそろえます
　今回学んだ一元配置の分散分析では反復数が個々の処理区で異なっていてもそれほど問題はありません．しかし，来週以降に学ぶより複雑な分散分析では，反復数が異なると解析が面倒になるだけでなく，精度も大きく落ちてしまいます．実験開始のときは反復数をそろえて実験するのが普通ですが，事故や不注意などで反復数がそろわなくなることもあるかもしれません．しかし，できるだけ反復のそろうように実験することが基本です．なお反復がそろわないからといって，一部のデータを削除するのは間違ったやり方です．

２．　複雑な実験はなるべく避けます
　前項とも関連しますが，分散分析ではデータが複雑になるほど，解析が面倒かつ間違えやすくなります．特にコンピューターで計算させるときは，データの入力の仕方を間違いやすくなり，自分の目的とする分散分析をするにはデータの構造が複雑（あるいはでたらめ）で，解析不能ということもあるかもしれません．そのうえ，反復がそろわなかったときの影響も大きくなります．必要のない複雑な実験は避けるのはもちろんのこと，必要だとしてもできるだけ簡単な実験計画にならないかをよく検討してから実験するべきです．実験計画を立てた時点で，どういう分散分析をするのかを決めておくのが正しい統計解析方法です．

３．　正規分布するデータが前提条件です
　分散分析では比較する母集団それぞれが正規分布すること，母分散が等しいことが理論的には前提条件になります．しかし，分散分析は多少その前提条件からはずれていても，結果が大きく左右されない頑健性をもっています．

４．　すべての水準に対して母分散が等しいことも前提条件です
　水準ごとの反復数がみな同じである場合，この前提が多少崩れても影響はあまりありません．