第1回 実験計画学とは?
1.実験して得たデータの解釈
実験をして得たデータの解釈をどうするかを考えてみましょう.
例えば,1) A,B,Cの3種類の餌を与えたヒツジの成長を調べた.どの餌がいちばんよいか?
2) 気温が上昇するとブドウの糖度はどうなるかを調べた.
データにはばらつきがあるので,1つや2つだけを調べてもそれが本当に正しいかは確信を持てません.ではデータをどのように取ったら確信を持ってもよいのでしょうか?
1)平均が知りたいなら何匹調べたらよいでしょうか?
これに対する答えは実験計画学第5回 統計的推定で説明します.
2)同じ形の池が2つあった.しかし,一方は富栄養化していて魚が大きくなったようだ.この仮説を証明するには2つの池からそれぞれ何匹を調べたらよいだろうか?
これに対する答えは実験計画学第6回 統計的検定で説明します.
池の中の魚の大きさを知りたいとしましょう.魚は池に百匹以上はいて,しかも正確な数はわかりません.魚の大きさは図のようにかなりまちまちです.
それ以前の人間(というよりは現代の人間でも大して変わりませんが)はごくわずかの経験で物事を決めてしまっていました.「柳の下のどじょう」のような話は今でもいくらでも聞くことができるでしょう.しかし,せいぜい2,3回の経験で物事を決めてしまうとあとでたいへんな過ちをおかすことは珍しくありません.農業の世界でも,1,2回の成功で,これでうまくいくと断言して,あとで災難を招いた例はいくらでも探せるでしょう.
しかし,たくさんのデータを集めて,解析すれば,少数の規則を発見できることがわかります.これが科学の黎明であったといえるでしょう.ケプラーの法則はさらにニュートンの万有引力の法則につながります.
惑星という漢字からイメージするところは,惑星というのは何らかの規則のある運動はしないように思えます.惑星は英語ではplanetですが,これも古代ギリシャ語を語源とし,その意味はさまよう(星)だそうです.昔の人は,惑星の動きに規則性を見いだせなかったということです.
1.惑星は太陽を焦点の1つとする楕円軌道上を動く.
2.惑星が一定時間に動径が描く面積は一定である(面積速度一定の法則).
3.惑星の公転周期の2乗は楕円軌道長径の3乗に比例する.
科学の始まりがいつからかは特定することはできないと思いますが,科学というものが形作られる上で特に取り上げなければならない発見にケプラーの法則をあげることができるでしょう.
ケプラー(1571-1630)の法則はブラーエ(1546-1601)による膨大かつ精密な天体観測記録から導き出されました.ブラーエの観測記録から火星の軌道をケプラーは長い年月をかけて導き出しました.ケプラーの法則は以下の3つです.
2.大数の法則
このように多数のデータから得た少数の規則は,むしろ新しい発見を導いたのです.さて,こういう自然科学だけでなく,人の寿命などでもたくさんのデータを集めれば規則性を導くことができます.特定の個人はいつ死ぬかわかりませんが,寿命に関するデータを集めて作られた生命表を見れば,日本人の男女がどんな割合で何歳まで生きられるかわかります.これを使って,生命保険などの掛け金が決まっていますし,年金などの社会福祉政策も決められます.また,個々人にしても,自分がいつ死ぬか明確にはわからなくても,だいたいいつぐらいまで生きられそうかはわかります.それをもとに人生設計していくわけです.(しない人の方が多いとは思いますが.)
このことから多数のデータを集めて規則性を得ることの意味がわかります.またいくら多数の数値を集めてもいい加減な数値(データとは呼べない)であれば,きちんとした規則性がでません.そんないい加減な数値から出た規則からはまともな政策もでないし,保険会社もつぶれてしまうでしょう.
さて,たくさんデータを集めれば,たくさんの規則性が得られるのならいいが,たくさん集めて,1つ2つの規則しか得られないなら大損だ・・・という人もいるでしょう.しかし,ケプラーの法則から導かれたニュートンの万有引力の法則から1846年に海王星が発見されました.海王星は1781年にハーシェルが発見した天王星の軌道がニュートンの万有引力の法則から計算されたものとずれていることから,その存在が予言され,その予言したほぼ近くに発見されたのです.
数多くデータを集めるとより正しい結論が得られるようになります.このようなことを述べた法則の一つに大数の法則があります.データをたくさん集めれば,集めるほど,そのデータの平均値は真の平均値に近づくという法則です.
最近は20歳代の事故は減少傾向にあり,一方,30歳代の事故が増加しているようです.ただ上のPDFのP23にあるように免許を持つ人について事故の割合を調べると若者の事故率の高さが際だちます.やっぱり保険料は高く設定されるのが合理的なのかもしれません.
例えば,自動車保険は20歳代の若者には高い掛け金が設定されています.それに対して,若者の方が反射神経も鋭く,運転ミスも少ないはず,なのに事故が多いはずの老人は掛け金が値上がりしないのに若者ばかり高い掛け金をとるのはおかしいという意見もあります.下の警察庁の交通事故調査をみてほんとのところはどうなのか,調べてみましょう
しかし,そうはいっても人間は誰しもけちですから,1,2回の経験で結論したがるものです.また,大数の法則にかなうだけのデータを集めるのが困難だったり,不可能だったりするものもあります.
1.自動車の耐久性テスト たくさんやればお金がかかりすぎる
2.オオサンショウウオの生態 そんなにたくさんいない
3.猫のエイズの治療薬 効くか効かないかわからない薬(それも劇物)をたくさんの猫に与えれば動物虐待といわれるかもしれない
などです.
3.でも少数のデータで何かをいいたい・・・
- 例1:犬の体重
- 犬の体重の平均はいくらでしょうか.自分の家の犬の体重が平均であるとはいえないでしょう.では何匹の犬をどのようにしてはかったら,犬の平均体重を推定できるでしょうか.
- 例2:猫のエイズの治療薬
- 日本の猫の12%が猫のエイズ(FIV)に感染しており,特別天然記念物のツシマヤマネコでは22%の感染率である*.このような猫のエイズの治療薬として,A,B,Cの3つを開発したとする.3匹の猫に3種類の薬を与える実験をして,それでこの薬は効きますと判断してよいのか.*猫のエイズについては集英社新書:猫のエイズ(石田卓夫著)に詳しい.
とりわけ農学,生物学,医学の対象とする生物を扱うとき,その測定量は大きなばらつきがあります.そのうえにたくさんのデータを集めるのがたいへんです.
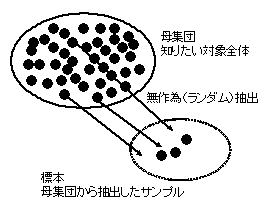
統計学は少数の標本であっても,その標本が母集団から無作為(ランダム)に抽出されたものであれば,その数が少なくても,ある程度の精度で結論できることを保証します.ここで大事なのは,自分の知りたい対象(母集団)から無作為に調査対象を抽出することです.少なくても無作為に選んだ標本の方が,数がいくらあろうと無作為でない標本よりははるかにまともな結論が出せるのです.
- 1.いくつサンプルをとればどのくらいの精度なのか.
- 犬の体重を何匹調べたらよいのか?その基準はあるのでしょうか.
- 2.どのようにサンプルを取ったらよいのか.
- 犬といってもいろんな種類があります.それに食生活が豊かな日本の犬だけを犬の代表にしてよいのでしょうか.猫のエイズの治療薬にしても発病してどのくらいたった猫かで薬の効果が違うでしょう.ひょっとしてAは発病直後にはよく効き,Cは末期症状を緩和するという効果があるのかもしれません.
- 3.たくさんのサンプルを取ること自体が難しい.
- 数を増やせば増やすほど,労力,時間,費用がかかります.実験の規模が大きくなると,実験を均一に行うことが難しくなります.動物実験ではあまりにたくさんの動物を使うことは倫理的な問題も関わってくるでしょう.
さて,生物について何かをいおうとするとデータがばらつくためにかなりの数を調べないといけないということになります.しかし,たくさんのデータを取ればよいというわけにはいきません.いくつかの問題点があります.
次に少ない実験でもできるだけの情報を取り出したいと考えます.
数が多くても偏った標本では正しい結論は得られません.上の図のように無作為に抽出された標本からは統計的手法を用いて,少数の標本であっても何らかの結論を得ることができます.標本数が少ないと確実さは小さくなりますが,結論自体は一定の範囲で出すことができます.
例えば,喫煙が健康に害があるかを無作為に抽出された100人の標本から結論を出せば,その結論はある程度の誤差はあるけれども有効なものです.一方,75歳以上の愛煙家が数百人,喫煙しない75歳以上の配偶者といっしょに集結し,たばこは健康の秘訣である,副流煙も健康にいい,なぜならここに集結しただけの健康な老人がいるからだといっても統計的にはあまり意味がありません.無作為に抽出された標本ではないからです.数万人集まったとしても同じことです(それでも高齢者人口の1パーセントにも達しないから)
ちなみに75歳以上の人口は1000万人を超えています.
さて,無作為に抽出された標本でないと正確なデータはえられないといいました.しかし,標本の選び方は難しいのも事実です.
標本に要求されることは以下の2つです.
1)母集団を代表しているか(統計的な手法を適用するための条件)
2)精度が必要な程度あるか(サンプルの数が多ければ精度は高くなる)
さて先ほどの愛煙家の例は極端にしても,標本が母集団をあまり代表していないことはよくあります.
例えば,インターネットを使って,世論調査したら・・・? → インターネットを使えない人(高齢者?,忙しい人?)は対象から抜けます.
元気そうなウシばかりサンプリングしたら? 畜舎に行って元気そうな牛から採血し,元気そうでないのはかわいそうだからと採血しなかったら・・・
★ 池の魚を調査する例をもう一度考えてみましょう.この池の魚で,大きな魚は底に住む性質があるとしましょう.もし調査のときに,面倒だからと水面近くの魚ばかり調査したらどうなるでしょうか?
農学実験ではいくつかの要因(気温,湿度,肥料,品種など)について同時にいろいろに変えて実験したいことがよくあります.気温2つ,湿度2つ,肥料2つ,品種2つとしただけでも16種類の組み合わせになります.こんなにたくさんの実験をやるのはたいへんです.こういう場合に上手に組み合わせて,データを解析してやれば実験を減らせます.実験計画学では実験回数を抑えながら,データの精度を高め,得られたデータからできるだけ多くの情報を得るためにはどのように実験を計画,組み立てればよいか,得られたデータをどう解析するかなどを学びます.
注意)ときどき実験が終わってからどうやってデータを解析したらいいのですかと聞きに来るのですが,実験を計画する段階ですでにデータの解析方法を考えておくのが正しいのです.だから実験計画学なのですね.
データの精度を見積もり,その上でいかに少ない実験回数あるいはサンプルで精度よくデータを得るかが大事になります.そのような方法を提供するのが統計学の1分野である実験計画学です.
実験計画学のメリットは大きく3つあります.
1.実験回数を少なくできる.
2.精度がよくなる.あるいは精度がわかる.
3.実験データの変動を解析できる.
1)何か法則性がありそうなデータを集めます.データを集める前に,どんな法則が出てくるかを予想します.
2)100 以上のデータを集め,大きさの順に並べます.
3)次の値を見つけだすあるいは計算します.
最大値,最小値,レンジ(最大値と最小値の差),平均,
メジアン(中央値:大きい順に並べたときまん中に来る値.データが偶数のときはまん中に位置する2つの値の平均)
4)分布をグラフにします(ヒストグラムの作成)
最大値と最小値の間を5,10,15 に分級してそれぞれ頻度分布を書きます.
5)ここまでの時点で観察の結果,わかったことを,最初の予想と照らし合わせながら書きます.箇条書きでよいから,なるべくたくさん書くのがよいです.なお上の2)〜4)の手順に基づいてデータをまとめていくとき,どの手順の時にわかったかをなるべく書くこと.
- イネの穂の長さ(連続データ)
- ニワトリの卵の重さ(連続データ)
- 大橋川に生えているヨシの草丈(連続データ)
- 映画に出演するエキストラの数(離散データ)
- 宍道湖のシジミの収穫個数(離散データ)
- 松江のスーパーで売られる豚肉の値段(離散データ)
1. 大数の法則を当てはめることのできるくらいのデータを集める.最低でも100以上のデータを集める.
なお調査テーマが大数の法則にはふさわしくないものなど以下の1)〜8)を満たさないものであればテーマをもう一度考え直させます.承認を得ないテーマで調べても,レポートは受け取りません.
次のような条件を満たしているデータでなければなりません.
1)個々のデータには誤差が含まれている.
車のナンバープレートなどはそれぞれの値がそれぞれ固有の値であり,誤差がありえない.
2)2,3のデータではデータ全体の特徴はよくわからないが,データ数を増やしていくとデータ全体の特徴が次第に明らかになっていく.
3)もしすべてのデータを調べるとデータ数が1万以上あること.
世界各国のGDP,市町村の人口などは1万以上はない.
4)得られたデータが母集団を代表すること.
世界の山の高さなど・・・得られたデータは標高の高い山ばかりだから世界の山を代表しない.上位100人のホームラン数なども同じく母集団を代表しない.
5)大数の法則に従わない時系列のデータではないこと.
1901 年から2000 年までの日本の人口,物価,交通事故数などは時間とともに変化するので,データを増やしてもその平均で何かを論じることはできない.地震の回数などは大数の法則に従うと考えることができるので調べてもよい.
6)離散データか連続データであること.
色,性別などのデータは,第2回目の授業で計算する平均,標準偏差などの計算をすることができない.したがって,以下の5種類のデータのうち,離散データもしくは連続データに属するものでなければならない.
データの種類は大きく,5つに分けられる.
名目データ:順序,大きさのない属性データ.例えば,性別,色,血液型など.
順序データ:順序,段階だけを示したデータ.大,中,小あるいは数字で1〜5(成績)など.
順位データ:順位を付けたデータ.
離散データ:とびとびの値をとるデータ.人数,個数,値段など.
連続データ:連続的な値を取るデータ.身長,速度,濃度など.
7)データの値について少なくとも50以上の異なる値をとりうること.したがって,松江市内の建物の階数,家の部屋の数,所持する靴の数などはだめである.
8)ほかの学生のテーマや授業やこのプリントで示した例に似ているものはだめである.賭け事および相場に関するものもだめである(麻雀,競馬,株価など).できるだけ目新しいテーマを考えるように.
度数分布を作るときに,階級の境界値はキリのいい値にしましょう.データによっては10や15に分級できないことがあります.その場合は,分級できる最大数で分級してください.
以下,エクセルを用いて1000個のデータを解析した例を示しました(ボタンを押してください).