戞10夞丂暘嶶暘愅偦偺俁丂幚尡寁夋丒棎夠朄丒儔僥儞曽奿朄
乮俀乯幚尡偵偲傕側偆岆嵎傪偳偆惂屼偡傞偐丠
丂僨乕僞傪庢傝埖偆幚尡偵偼岆嵎偑昁偢晅悘偟傑偡丏偙偺岆嵎傪偄偐偵惂屼偡傞偐偑幚尡偱摼傜傟偨僨乕僞偺惓妋偝丆怣棅惈傪崅傔傞忋偱廳梫偱偡丏岆嵎偼戝暿偡傞偲丆宯摑岆嵎偲嬼慠岆嵎偵暘偗傜傟傑偡丏偙偺偆偪宯摑岆嵎偼曃傝傪帩偭偨岆嵎偱偁傝丆偙偺宯摑岆嵎傪偄偐偵彫偝偔偡傞偺偐傪峫偊偰傒傑偟傚偆丏
丂傑偢宯摑岆嵎偲偼偳傫側傕偺偱偟傚偆偐丏
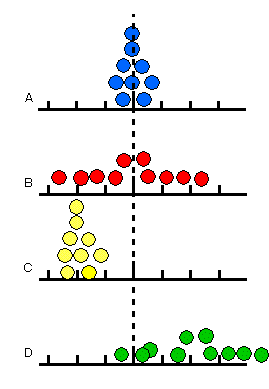
丂塃偺恾傪尒偰偔偩偝偄丏俙丆俛丆俠丆俢偺係恖偑偁傞應掕傪壗夞偐孞傝曉偟傑偟偨丏恀偺抣偼揰慄偱帵偟偰偁傝傑偡丏俙丆俛偼暯嬒偼恀偺抣偵嬤偄偺偱偡偑丆俛偼僨乕僞偺偽傜偮偒偑戝偒偄傛偆偱偡丏堦曽丆俠丆俢偼暯嬒傕恀偺抣偐傜奜傟偰偄傑偡丏偝偰丆俛偲俠偱偼偳偪傜偺暘愅偑傛偄偺偱偟傚偆偐丏
丂傕偟丆俠偺抣傪曗惓偡傞庤偩偰偑側偗傟偽丆俛偺曽偑暘愅偼傛偄偙偲偵側傝傑偡丏側偤側傜丆俛側傜偽幚尡夞悢傪憹傗偣偽丆恀偺抣偵暯嬒偑嬤偯偒傑偡偑丆俠偼偄偔傜幚尡傪偟偰傕恀偺抣偵偼嬤偯偒傑偣傫丏宯摑岆嵎偲偼偙偺傛偆側俠偺弌偡岆嵎偩偲偄偊傑偡丏偄偔傜戝悢偺朄懃偱偨偔偝傫僨乕僞傪廤傔傟偽恀偺抣偵嬤偯偔偲偄偭偰傕丆宯摑岆嵎偼僨乕僞傪憹傗偟偰傕彫偝偔側傜側偄偺偱偡丏
丂偡側傢偪宯摑岆嵎偑偁傝丆偦傟偵婥偯偐側偗傟偽丆暘嶶暘愅偟偰摼傜傟傞岆嵎偵偼宯摑岆嵎偑擖傜側偄偙偲偵側傝丆僨乕僞偺夝庍傪戝偒偔娫堘偭偰偟傑偄傑偡丏
丂偟偨偑偭偰丆岆嵎慡懱傪彫偝偔偡傞埲慜偵丆宯摑岆嵎傪尭傜偡丆側偔偡丆偦偟偰尭傜偣側偄応崌偵偼嬼慠岆嵎偵揮壔偡傞偙偲偑昁梫偵側傝傑偡丏偦偺曽朄傪帵偡偺偑丆僼傿僢僔儍乕偺嶰尨懃偱偡丏
丂嬶懱揑偵偼宯摑岆嵎偼偳偺傛偆側傕偺偑偁傞偱偟傚偆偐丏梤偱幚尡偡傞偲偟傑偟傚偆丏10摢偺摨偠昳庬偺梇偺梤傪廤傔偨偲偟偰傕丆楊丆懱廳丆恊偺堚揱偦偺懠偄傠偄傠側梫慺偑幚尡傪嵍塃偟偦偆偱偡丏幚尡偡傞偲偒偵宯摑岆嵎傪弌偡偲傢偐偭偰偄傞傕偺偼偁傜偐偠傔彍嫀偡傞偺偑傛偄偺偱偡偑丆懱廳丆楊側偳偺慡偔摨堦側梤傪10摢傕廤傔傞偙偲偼尰幚揑偱偼偁傝傑偣傫丏偁傞偄偼宯摑岆嵎偼弌傞偺偩偗傟偳丆惂屼偳偙傠偐丆宯摑岆嵎偺尨場偺掕偐偱側偄傕偺傕偁傝傑偡丏曓応偺抧椡儉儔丆暘愅婡夿偺擔傗帪娫偵傛傞旝柇側曄摦側偳偼宯摑岆嵎傪惗傒傑偡偑丆尨場傪徻偟偔挷傋傛偆偲偡傞偺偼庤悢偱偡丏
僼傿僢僔儍乕偺嶰尨懃偱偼偙偺傛偆側宯摑岆嵎傪惂屼偡傞偨傔偵傑偢
侾丏斀暅
丂岆嵎傪尒愊傕傞偙偲偑偱偒側偄偲丆惂屼偡傞偵傕惂屼偱偒傑偣傫丏岆嵎傪抦傞偵偼彮側偔偲傕摨偠忦審偱幚尡傪暋悢孞傝曉偡昁梫偑偁傝傑偡丏偙傟傪斀暅偲偄偄傑偡丏
丂偝傜偵斀暅傪憹傗偡偲丆暯嬒偵偮偄偰偺岆嵎偱偁傞昗弨岆嵎偦偺傕偺傕彫偝偔側傝傑偡丏
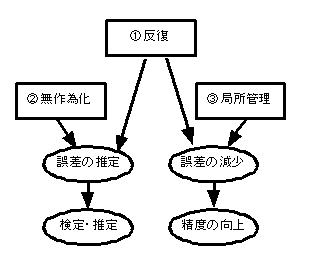
丂偡側傢偪丆斀暅傪愝偗傞偙偲偵傛偭偰丆岆嵎偺昡壙偲岆嵎偺尭彮偺俀偮偑幚尰偟傑偡丏
僼傿僢僔儍乕偺嶰尨懃偱偼壓偺恾偺傛偆偵俁偮偺尨懃偑偦傟偧傟岆嵎偺悇掕偲尭彮偵栶棫偪丆岆嵎傪悇掕偡傞偙偲偱暘嶶暘愅偺傛偆偵摑寁揑専掕丒悇掕偑弌棃丆岆嵎傪尭彮偡傞偙偲偵傛偭偰惛搙傪岦忋偡傞偙偲偑偱偒傑偡丏
俀丏柍嶌堊壔
丂宯摑岆嵎偺偁傞僨乕僞偵暘嶶暘愅側偳偺摑寁揑庤朄傪揔梡偟偰傕惓偟偄寢壥偼摼傜傟傑偣傫丏宯摑岆嵎傪偱偒傞偩偗嬼慠岆嵎偵揮壔偡傞曽朄傪柍嶌堊壔偲偄偄傑偡丏椺偊偽丆梤偼屄懱偵傛偭偰塧偵懳偡傞斀墳偑堘偆偐傕偟傟傑偣傫丏梌偊傞塧傪偳偺梤偵梌偊傞偐傪柍嶌堊偵乮儔儞僟儉偵乯寛傔傞偙偲偵傛偭偰丆梤偺屄懱娫嵎堎偵婎偯偔宯摑岆嵎偼柍嶌堊壔偝傟傑偡丏
椺偊偽梤偺懱廳偵傛偭偰丆寢壥偑曄傢傞偲偟傑偟傚偆丏彫偝偄懱廳偺梤俁摢偵俙丆戝偒偄懱廳偺梤俁摢偵俛偺栻傪梌偊傞側傜丆偦偺寢壥偵偼宯摑岆嵎偑擖傝崬傒傑偡丏偙偆偄偆宯摑岆嵎偼愭傎偳偺恾偺俠偺寢壥偲摨偠偔丆僨乕僞偺尒偐偗偺偽傜偮偒傪彫偝偔偡傞乮側偤側傜丆懱廳偺嬤偄梤偺僨乕僞偼傛傝偽傜偮偒偑彫偝偄偐傜乯偐傜傛偗偄偵夝庍傪娫堘偆偙偲偵側傝偐偹傑偣傫丏懱廳偵娭學側偔丆柍嶌堊偵幚尡偡傞偲懱廳偺偪偑偄偵傛傞岆嵎乮宯摑岆嵎乯傪嬼慠岆嵎偵揮壔偡傞偺偱丆僨乕僞偺尒偐偗忋偺岆嵎偼戝偒偔側傝傑偡丏偟偐偟丆柍嶌堊壔偟偨寢壥丆嬼慠岆嵎傪暘嶶暘愅側偳偱昡壙偱偒傞偺偱丆幚嵺偵偼幚尡偺専弌椡偼崅傑傝傑偡丏
丂椺偊偽丆掕検暘愅偺応崌偱傕俙丆俛丆俠偺俁偮偺僒儞僾儖傪俁夞斀暅應掕偡傞偲偒偵丆俙丆俙丆俙丆俛丆俛丆俛丆俠丆俠丆俠偺弴偱暘愅偡傞恖偑懡偔偄傑偡丏偙傟傕尒偐偗忋偼岆嵎偼彫偝偔側傝傑偡偑丆暘愅偺偲偒偺廃傝偺娐嫬乮壏搙丆帋栻丆婍嬶乯偺塭嬁偵傛傞宯摑岆嵎傪嬼慠岆嵎偵揮壔偟偰偄側偄偐傜恀偺抣偐傜戝偒偔偢傟偰偟傑偆婋尟偑偁傝傑偡丏俋夞偺暘愅傪柍嶌堊偵峴偆傋偒偱偡丏偦偺応崌丆尒偐偗忋僨乕僞偺岆嵎偼戝偒偔側傝傑偡偑丆偦傟偼幚尡偺偳偙偐偵宯摑岆嵎偺尨場偑偁傞偙偲傪帵偡傛偄徹嫆偱偁傝丆偝傜偵幚尡偺惛搙傪崅傔傞婡夛傪梌偊傜傟偨偲偄偆偙偲偵傕側傝傑偡丏
俁丏嬊強娗棟
丂僼傿僢僔儍乕偺嶰尨懃偺嵟弶偼斀暅偱偁傞傛偆偵丆斀暅偑側偄幚尡偼岆嵎傪昡壙偟傛偆偑側偔丆僼傿僢僔儍乕帺恎偼偦偆偄偆偺偼幚尡偱偼側偔丆偨偩宱尡傪憹傗偟偨偵偡偓側偄偲僐儊儞僩偟偨傜偟偄偔傜偄丆斀暅偼嵟傕戝帠側偺偱偡偑丆斀暅傪憹傗偡偲岆嵎傪暿偺堄枴偱憹傗偟偰偟傑偆壜擻惈偑偁傝傑偡丏愭傎偳柍嶌堊壔偺椺偱嫇偘偨傛偆偵丆梤偺摢悢傪憹傗偡偙偲偼丆斀暅傪憹傗偡偙偲側偺偱偡偑丆慡偔摨偠梤偑偙偺悽偵偄側偄埲忋丆梤偺屄懱偵傛傞嵎偼岆嵎傪憹壛偝偣傞偙偲偵側傝傑偡丏掕検暘愅偱傕壗夞偐偺暘愅傪偡傞偨傔偵壗帪娫傕幚尡偡傞偆偪偵丆幚尡偺応偺旝柇側曄摦偵傛偭偰丆岆嵎偑憹戝偡傞壜擻惈偑偁傝傑偡丏
丂偙偺傛偆偵斀暅傪憹傗偡偲偒偺岆嵎偺曄摦傪丆梤偱偁傟偽懱廳偺嬤偄傕偺傪丆暘愅偱偁傟偽帪娫揑偵嬤偄偁傞晹暘乮屵慜偲偐屵屻偲偐乯偵丆幚尡偱斾妑偟偨偄侾慻傪摉偰傞偙偲偵傛偭偰丆岆嵎傪偦偺晹暘偺堘偄偵揮壔偟偰丆彍嫀偡傞偙偲偑偱偒傑偡丏偙傟傪嬊強娗棟偲偄偄丆偙偺傛偆側偱偒傞偩偗嬒堦偵偟偨幚尡偺応偺堦晹傪僽儘僢僋偲偄偄傑偡丏
丂幚尡寁夋朄偱偼丆宯摑岆嵎傪偙偺傛偆側嬊強娗棟偵傛偭偰丆僽儘僢僋娫偺嵎偵偡傞偩偗偱側偔丆暘嶶暘愅偵傛偭偰丆僽儘僢僋娫偺岆嵎乮偡側傢偪僽儘僢僋偵偟偨寢壥丆彍嫀偱偒偨岆嵎乯傕掕検偱偒傑偡丏
係丏棎夠朄偺暘嶶暘愅
丂僼傿僢僔儍乕偺嶰尨懃傪枮偨偡婎杮揑側幚尡寁夋傪棎夠朄偲偄偄傑偡丏棎夠朄偱偼擇尦攝抲偲摨偠傛偆偵暘嶶暘愅偱偒傑偡丏偡側傢偪梫場偺堦偮傪僽儘僢僋場巕偲峫偊丆偙偙偱峫偊傞場巕偲偺擇尦攝抲偱峫嶡偡傞偙偲偵側傝傑偡丏僽儘僢僋場巕偼惂屼場巕傗昗帵場巕偲岎屳嶌梡偑側偄偙偲偑慜採偱偡偺偱丆棎夠朄偺応崌丆孞傝曉偟偺側偄擇尦攝抲偱偁偭偰傕偐傑偄傑偣傫丏
俆丏儔僥儞曽奿朄
丂僽儘僢僋場巕偑俀偮偁傞偲偒偼儔僥儞曽奿朄偵傛偭偰丆幚尡傪攝抲偟傑偡丏儔僥儞曽奿朄偺暘嶶暘愅偼僄僋僙儖偺暘愅僣乕儖偱偼偱偒傑偣傫丏捛壛偺僾儘僌儔儉傪庤偵擖傟傞偐丆傛傝崅搙側摑寁夝愅僜僼僩偱儔僥儞曽奿朄偺暘嶶暘愅傪偡傞偙偲偵側傝傑偡丏
俇丏廻戣
俙丏師偺幚尡傪攝抲偣傛丏側偍丆攝抲偼柍嶌堊偵偡傞偙偲丏
嘥丂俁昳庬乮俙丆俛丆俠乯偺悈堫偺廂検斾妑傪係僽儘僢僋偺棎夠朄偱幚尡偡傞丏
嘦丂庽楊乮俁丆俇丆俋丆侾俀擭乯偲曓応偺崅掅乮崅丆拞丆掅丆掙乯偺俀偮偺僽儘僢僋場巕偵傛偭偰丆奰偺係偮偺嵧攟曽朄乮俙丆俛丆俠丆俢乯傪斾妑偡傞乮庽楊偲嵧攟曽朄偵偼岎屳嶌梡偑側偄偲偡傞乯丏
侾丏幚尡寁夋朄
丂幚尡寁夋妛偱庢傝埖偆幚尡偵偼師偺俀偮偺摿挜偑偁傝傑偡丏
乮侾乯丂偄傠偄傠側忦審傪恖堊揑偵愝掕偟偰丆偦偺寢壥偺斾妑傪栚揑偲偡傞幚尡偱偁傞
乮俀乯丂摨偠忦審偺壓偱幚尡傪孞傝曉偟偰傕丆寢壥乮僨乕僞偱帵偝傟傞乯偼昁偢偟傕堦掕偱偼側偔丆偐側傝偺偽傜偮偒傪帵偡丏
乮侾乯偵偮偄偰偼丆埲壓偱偳偺傛偆側忦審傪愝掕偡傞偙偲偑偱偒傞偺偐丆偝傜偵忦審偼侾偮偩偗偲偼尷傜偢丆暋悢偺忦審傪愝掕偡傞幚尡偑昁梫側応崌偑偁傝丆偦偺偲偒偺偦傟偧傟偺忦審偺摿挜傪峫偊傑偡丏
乮俀乯偵偮偄偰偼幚尡偱偼愝掕偡傞忦審埲奜傪嬒堦偵偐側傜偢偱偒傞傢偗偱偼側偔丆偦偺傛偆側晄嬒堦偝偑尨場偱岆嵎偑惗偠傑偡丏偄偐偵偟偰岆嵎傪彫偝偔偡傞偐丆偁傞偄偼幚尡寢壥偵曃傝偺側偄傛偆側岆嵎偵揮壔偡傞偐傪埲壓偱弎傋傑偡丏
偡側傢偪幚尡寁夋朄偺栚揑偼
乮侾乯丂幚尡偱庢傝埖偆場巕乮梫場乯傪揔愗偵慖戰偡傞偙偲
乮俀乯丂幚尡偵偮偒傕偺偱偁傞岆嵎傪惂屼偡傞偙偲
偱偡丏
俀丏場巕偲悈弨
丂幚尡偵偍偄偰偦偺忦審傪庬乆偵曄偊偰斾妑偡傞傕偺傪場巕偲偄偄丆場巕偺庢傝偆傞忦審傪悈弨偲偄偄傑偡丏
椺偊偽丆悈堫偺嵧攟幚尡偱偼丆場巕偲偟偰丆昳庬傗巤旍検側偳傪峫偊傞偙偲偑偱偒傑偡丏
| 場巕 |
悈弨 |
| 昳庬 |
僐僔僸僇儕丆僴僫僄僠僛儞丆僸僲僸僇儕 |
| 巤旍検 |
0, 4, 8, 12g/m2 |
丂場巕偼戝偒偔埲壓偺係偮偵暘椶偱偒傑偡丏
乮侾乯惂屼場巕丂偦偺嵟揔忦審乮悈弨乯傪抦傞偨傔偵庢傝忋偘傞場巕
乮俀乯昗帵場巕丂惂屼場巕偲岎屳嶌梡偑偁傞偨傔偵庢傝忋偘傞場巕偺偆偪丆幚尡偺応偱偼惂屼偱偒傞場巕
乮俁乯僽儘僢僋場巕丂嬊強娗棟偵梡偄傞場巕丏懠偺場巕偲岎屳嶌梡偼側偄丏
乮係乯憌暿場巕丂幚尡偺応偱傕惂屼偱偒側偄偑丆懠偺場巕偲岎屳嶌梡傪帩偮場巕丏
丂椺偊偽丆搰崻導偱傕偭偲傕懡廂偲側傞悈堫偺昳庬傪寛傔傞幚尡傪偡傞側傜丆惂屼場巕偼昳庬偲側傝傑偡丏偲偙傠偑昳庬偲偄偆場巕偼巤旍傗嶌婜偲偄偆場巕偲岎屳嶌梡偑偁傞偙偲偑傢偐偭偰偄傑偡丏傕偟巤旍傗嶌婜傪擾壠偑幚嵺偺尰応偱帺桼偵慖傋傞側傜偽巤旍傗嶌婜傕惂屼場巕偵娷傔偨幚尡傪偟傑偡丏偟偐偟丆偨偲偊偽幊摴屛偺晉塰梴壔懳嶔偱巤旍傪帺桼偵慖傋側偄丆偁傞偄偼悈棙偺娭學忋丆揷怉偊偺帪婜乮嶌婜乯傪帺桼偵慖傋側偄側傜丆巤旍傗嶌婜偼擾嬈帋尡応偱偼惂屼偱偒傑偡偑丆尰応偱偼惂屼偱偒側偄昗帵場巕偲偄偆偙偲偵側傝傑偡丏偝傜偵擭偵傛偭偰丆偁傞偄偼嶻抧偵傛偭偰廂検偑堎側傝丆昳庬偲岎屳嶌梡偑擣傔傜傟傞側傜丆偦傟偼幚尡偺応偱傕惂屼偱偒側偄偺偱丆憌暿場巕偲偄偆偙偲偵側傝傑偡丏
丂幚尡偱柧傜偐偵偟偨偄場巕偲悈弨傪柧妋偵偟偨傜丆偦偺場巕偲岎屳嶌梡偺偁傞場巕偺偆偪丆尰幚揑偵廳梫側傕偺偑側偄偐傪傛偔峫偊傑偟傚偆丏
俁丏岆嵎偺惂屼
乮侾乯暘嶶暘愅偲岆嵎
丂愭傎偳弎傋偨場巕偑岠壥偑偁傞偺偐傪抦傞摑寁揑庤朄偑暘嶶暘愅偱偡丏暘嶶暘愅偱偼庡岠壥傗岎屳嶌梡偺戝偒偝傪岆嵎曄摦偲斾妑偡傞偺偱丆岆嵎傪彫偝偔偱偒傟偽専弌椡偑崅傑傝傑偡丏偱偼偳偺傛偆偵偟偨傜岆嵎傪偪偄偝偔偱偒傞偱偟傚偆偐丠偟偐偟丆偦偺慜偵岆嵎偺庬椶偵偮偄偰峫偊側偗傟偽側傝傑偣傫丏
俛丏偙傟傑偱偵擇尦攝抲偺暘嶶暘愅傑偱傪妛傫偱偒偨丅擇尦攝抲偱偼場巕偼俀偮偱偁傞偑丄場巕悢偑偝傜偵懡偔偰傕暘嶶暘愅偼壜擻偱偁傝丄俁偮埲忋偺場巕偺偁傞応崌偼丄懡尦攝抲偲偄偆応崌偑偁傞丅場巕悢偑係偮埲忋偺幚尡傪峫偊偰尒傛丅偦傟偧傟偺場巕偵偮偄偰丆惂屼場巕丆昗帵場巕丆僽儘僢僋場巕丆憌暿場巕偺偳傟偐傪峫偊偰傒傛丏偝傜偵壖偵偙偺係偮埲忋偺場巕偡傋偰偵偦傟偧傟岎屳嶌梡偑偁傞偲偟偨傜丆偳偺傛偆側岎屳嶌梡偑峫偊傜傟傞偐傪偡傋偰彂偒弌偟偰尒傛丅
椺丗乮偨偩偟場巕悢偼俁偮乯
丂悈堫偺巤旍幚尡偱拏慺偺巤旍乮桳柍乯丄儕儞巁偺巤旍乮桳柍乯丄僇儕偺巤旍乮桳柍乯偺俁偮偺場巕偱幚尡偟偨丅岎屳嶌梡偼拏慺偲儕儞巁丄拏慺偲僇儕丄儕儞巁偲僇儕丄拏慺偲儕儞巁偲僇儕偺係庬椶偑峫偊傜傟傞丅