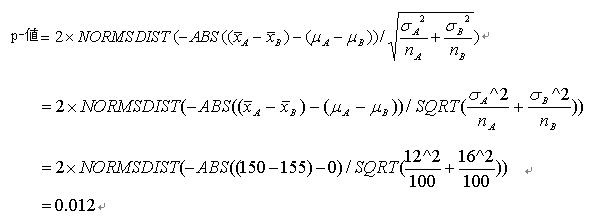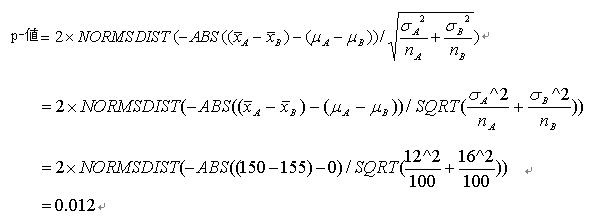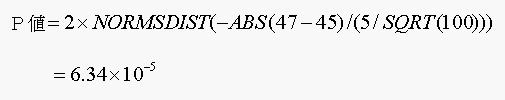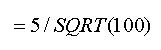6.統計的検定の手順のまとめ
1.帰無仮説をたてます.
2.対立仮説をたてます.ふつうは両側検定とします.
3.有意水準を決める.
有意水準は統計的検定の計算を始める前に決めます.可能ならば実験を始めたり,データを集めたりする前に決めるのが望ましいです.とくに統計によって何らかの判断を検定結果から行うときは有意水準を事前に決めなければなりません.p-値をみてから有意水準を決め,判断するというのでは,統計的な方法をつかわないで恣意的にカンで物事を決めるのとほとんど同じことだといえるでしょう.
統計による判断を実験した人が行わないで,ただデータをつけて結果の提示だけを行うときにはデータにp-値あるいは有意差を示す記号を付けます.p-値をつけるのがより明確ですが,以前はp-値の計算が面倒であったので,慣例として有意差を示す記号を付け,*は5%水準で,**は1%水準で,***は0.1%水準で有意差があることを示すことが一般的です.しかし,この記号は慣例で使われているだけなので,確認して使うべきでしょう.
4.p-値を計算する.
特に有意水準について断りのない場合は,有意水準を5%として,得られたp-値について以下のように結論するのが一般的です.
0.05<p-値 5%の有意水準で帰無仮説は棄却できず,対立仮説の否定を採用する.
0.01<p-値≦0.05 5%の有意水準で帰無仮説は棄却され,対立仮説を採用する.
0.001<p-値≦0.01 1%の有意水準で帰無仮説は棄却され,対立仮説を採用する.
p-値≦0.001 0.1%の有意水準で帰無仮説は棄却され,対立仮説を採用する.
5.統計的検定を行う.
p-値が最初に決めた有意水準よりも小さければ,帰無仮説は棄却され,有意差があると判断できます.帰無仮説が棄却できないときは「差があるとはいえない」という結論になります.帰無仮説を採用して,「差がない」という結論にしてはいけません.
6.現実的な意味での差があるかの判断
統計的に有意差があることと現実的な意味でその差に意味があるかというのは別問題です.すなわちp-値が小さければ小さいほど,差があることを統計的に強く確信が持てるとはいえます.しかしp-値が小さければ小さいほど,現実的な意味での価値が増すというわけではありません.
3.第1種の誤りと第2種の誤り(有意水準と検出力)
1)第1種の誤り
帰無仮説が正しいにもかかわらず,これを否定する過誤を第1種の誤りといいます.さいころの例では,本当はさいころは正しくできているのに,たまたま5回続けて奇数が出ることもあり,このときに第1種の誤りを犯すことになります.すなわち不良品でないのに,不良品という判断を下したことになります
第1種の誤りを犯す危険率を有意水準といい,αで表すことがあります.有意水準を小さくして,検定すれば,第1種の誤りを犯す危険は小さくなります.さいころの例でいえば,,10回続けて奇数が出なければ,帰無仮説を否定しないとすれば,有意水準0.001で検定したことになり,そういうことは1000回に1回しかないので,帰無仮説を否定できると結論できます.
今回のデータからp-値を計算すると,以下のようになります.
例: あるメーカーではさいころを作っており,5回振って出た目をチェックして正確なさいころであるかをチェックしている.あるさいころを5回振ったところ,5回とも奇数だった.二項分布から5回とも奇数になる確率は1/32(=0.03125)である.このような低い確率が出ることから,さいころは奇数と偶数が同じ確率で出ると考えるよりも,奇数が出やすいと結論し,そのさいころは不良品と判断した.
したがって,有意水準5%で帰無仮説は棄却され,2つの農場のみかんの重さ(の母平均)は異なると結論できます.
例:2つの農場のみかんについて100個ずつ調査し,農場Aは150±12g,農場Bは155±16gを得た(平均±標準偏差).両農場のみかんの重さ(の平均)は異なるのかを検定せよ.
2.正規分布に基づく検定
|
本当に成り立っているのは |
| H0 |
H1 |
| 検定結果 |
H0 |
正しい
(その確率:1-α) |
第2種の誤り
(その確率:β) |
| H1 |
第1種の誤り
(その確率:α:有意水準) |
正しい
その確率:1-β=検出力 |
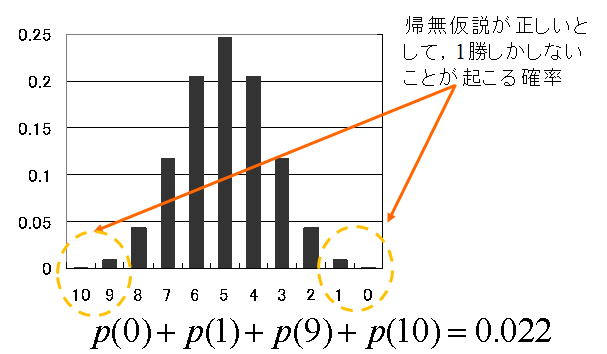
有意水準を5%とすると,帰無仮説が成り立つとしたときにA君が1勝あるいは0勝である確率は0.022となります.したがって,帰無仮説は棄却され,A君はキャラクターBと互角ではない,勝つ確率は0.5ではないといえます.
エクセルで計算すると以下のようになります.
注意)
A君が1勝9敗となる確率だけで計算してはいけません.例えば勝負を1000もやればちょうど500勝500敗になることのほうがきわめてまれになります.互角だとすると,1勝しかできないような極端な負け方をする確率はどのくらいであるかを考えるので,0勝および1勝だけでなく,10勝,9勝も含めたの4つの場合を合計します.これを両側検定といい,ここで得たp値を両側確率といいます.
2)二項分布に従うとすると,帰無仮説が成り立つとした場合,A君が1勝9敗となる確率は以下のように計算できます.
例題:
A君は対戦型ゲームでキャラクターBと互角に戦えると主張しているが,実際やってみると1勝9敗だった.A君の主張の真偽を統計的に検定せよ.
上の例では,母数について奇数と偶数が同じ確率で出るという予想をたて,それを否定しているので,これは統計的検定です.検定の手順は次のようになります.
帰無仮説:2つの母集団の平均の差は0,2つの母集団の平均は等しいということですから,ここでは品種Aと品種Bの1穂穎花数は等しいということになります.一方,対立仮説は2つの母集団の平均の差は0ではない,2つの母集団の平均は異なるということですから,品種Aと品種Bの1穂穎花数は異なるということになります.
この場合,2つの標本の平均の差が0であるという帰無仮説を検定します.2つの母集団がお互いに独立しているならば,2つの標本の平均の差も正規分布に従います.2つの母集団が独立しているとは母集団Aの値とは全く関係なく,母集団Bの値が決まることです.例えば,気温と部屋の温度の2つはお互いに関係がありそうですから独立していません.対になっているデータの場合は,独立していると,あとの授業で学びますが,相関係数が0となります.
標本平均は標本の大きさが十分に大きければ正規分布に従います.そこで正規分布の性質から標本から得た統計量を利用して,母集団に関する統計的な検定をすることができます.
例えば,次の例を考えてみましょう.
1)帰無仮説と対立仮説を立てます.
この場合,
帰無仮説は「A君はキャラクターBと互角に戦う」すなわち「A君がキャラクターBに勝つ確率は0.5である」,
対立仮説は「A君はキャラクターBより弱い(互角でない)」すなわち「A君がキャラクターBに勝つ確率は0.5でない」
2.二項分布を利用した統計的検定(実際にはこんな仕方での検定はしません.あくまで検定とはどういう思想を元にしているのかを説明するためのモデルとしてこの節は読んでください.)
さいころの例でいえば,さいころで奇数と偶数が同じ確率で出るとしたら,今回の結果のように奇数が5回出ることはきわめてまれであると考えます.したがって,元の仮定である「このさいころでは奇数と偶数が同じ確率で出る」は疑わしいと結論するわけです.統計的検定ではこのように数値的に明確な仮説から得られる確率を実際に得たデータと比較して,どのくらいありそうかを判断します.だから,はじめから,この確率でこのさいころでは奇数が出るとしても,証明しようがないのです.
対立仮説を証明したいのに,帰無仮説のようなものを持ち出すのはまどろっこしく感じるかもしれません.しかし,統計的にできるのは帰無仮説の否定だけです.その理由は以下の2つです.
★ 「甲は乙より速い」といっても,どのくらい速いのか,甲が乙に勝つ確率はいくらなのか,がはっきりしない.これを明確に規定できなければ,数量的に取り扱えない.
★ 仮に仮説を数量的に規定できても,それが真実であることを統計的には証明できない.統計的にできることは,仮説に対する「反証」を提示することだけである.
1)帰無仮説の設定
統計的検定によって否定したい仮説を立てます.これを帰無仮説といいます.前述の例ではこのさいころは奇数と偶数の目が同じ確率で出るというのが帰無仮説になります.
帰無仮説が成り立つとしたら今回の2つの標本が得られる確率(P値)を計算します.
ここでは2つの標本からえた標準偏差を1つにする必要があります.2つの独立した母集団では1つの母集団にすると,分散は両分散の和になるという性質があります.このことから次のことがいえます.
帰無仮説が成り立つとしたら今回のような標本平均が得られる確率は1%よりも小さく,帰無仮説が正しいとするとめったに起こらないことになります.したがって,帰無仮説(卵の重さは変わらなかった)の反証が示されたと考え,帰無仮説は棄却され,対立仮説を採用します.
例: 枕木養鶏舎では平均45gの卵を集荷している.枕木山の木を伐採し,鶏舎の日当たりをよくした.その結果,卵100個を調査すると,平均47g,標準偏差5gとなった.卵の重さは変化したのだろうか.
有意水準を小さくすれば,第1種の誤りをおかす危険性(不良品のさいころでないのに不良品として扱う確率)は小さくなります.しかし,第2種の誤り(不良品のさいころなのに見逃す確率)をおかす危険性は大きくなります.統計的検定では有意水準を決めることによって,第1種の誤りの大きさを制御しています.すなわち第1種の誤りを避けることに重点が置かれています.このことは統計的検定では貴重な発見(ここでは不良品のさいころをみつけることが科学的な新発見に対応する)を見落としてしまってでも疑わしい結果を受け入れることを避けているといえます.
2)第2種の誤り
しかし,5回続けて奇数の出るさいころが正しいさいころであるよりは,奇数の出やすいさいころと考える方がありそうです.このように帰無仮説が誤りであるにもかかわらず,これを否定しない過誤を第2種の誤り(さいころの場合,不良品なのにそれを見逃す確率)といいます.第1種の誤りを減らすために有意水準を小さくすれば,第2種の誤りの危険率(β)は高くなる,すなわち検出力(1-β)は低下します.帰無仮説をH0,対立仮説をH1とすると,2種類の誤りと検定結果には下の表のような関係があります.
3)下のグラフの点線で囲んだ部分が今回のような結果が起こる確率だと考えられます.
2)対立仮説の設定
もし帰無仮説が棄却されたときに採用される対立仮説を設定します.前述の例では奇数と偶数の目が同じ確率では出ないというのが対立仮説です.もしくは奇数の目が偶数の目より出やすいという対立仮説を立てることもあります.
(2) 2つの独立した母集団から得た2つの標本平均についての検定
さきほど学んだように統計的検定でできるのは仮説の反証を示すことだけです.ここで仮説は検証可能な仮説である卵の重さの母平均に変化はなかったということです.卵の重さの母平均に変化はなかったのにもかかわらず,今回のデータを得る確率はいくらかを計算し,その確率がある一定の確率以下であれば,元の仮説(帰無仮説)がむしろ間違っていると判断し,対立仮説(卵の重さは変化したあるいは増加した)を採用するのです.
このように統計的検定では帰無仮説に対する反証を示すことで対立仮説が正しいとする方法をとります.
3.帰無仮説が成り立つとしたら今回の標本平均が得られる確率(p-値)を求める.
2.必要なデータは何かを確認する.
まず,帰無仮説は卵の重さは変わらなかったというのですから,卵の重さの平均は45g,標準偏差は5gということになります.一方,今回のデータは卵の重さの平均は47gです.データの数は100個です.従いまして,今回のデータの卵の重さの標準誤差は
3)統計的検定を行うときの有意水準を決めます.ふつうは5%,1%あるいは0.1%が使われます.次に統計的検定に必要な統計量を集めます.そして,その統計量から帰無仮説が成り立つとしたら,今回得たデータが出現する確率(有意確率,p-値)を求めます.
5)p-値が宣言した有意水準よりも高いときは,帰無仮説を棄却できるだけの有意差がない(証拠がない)ということになり,有意差が認めらなかったと判断します.なお帰無仮説が棄却できないというのは帰無仮説を採用するということではありません.
したがって,結論は「差があるとはいえない」というような言葉遣いとなります.
4)p-値が宣言した有意水準よりも低いときは,帰無仮説が成り立たない(これを帰無仮説を棄却するといいます)と判断し,対立仮説を採用します.
エクセルで標準誤差SEを計算するには以下のようにします.