プログラミング入門II 宿題 2025.06.11

Back

最小2乗法を利用して直線の近似式を求めることを行ってみましょう．手順は以下のように行います．

  1. データの準備

    2. 添付のモジュール make_list.py を使用してデータを生成しますので，本体の中でそのモジュールを読み込んでリストデータを作ってください．

    作成されるデータは2次元リストになっていますが，後々総和の計算が楽になるように，10個の x データと同じく10個の y データがそれぞれまとめて内側のリストになっています．

  2. 最小2乗法を使った近似直線の求め方

    3. 求める近似曲線の式を y = a + bx とすると，係数 a と b は以下の式で求められます．

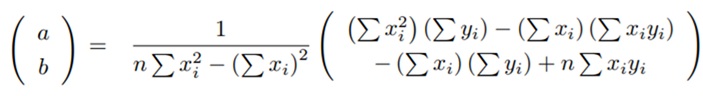
    ここで，n はデータの組の個数（今回は10），xi と yi はそれぞれのデータです．

    この式は学生実験のテキストに載っているものと同じです．
  3. 本体プログラム

    4. make_list モジュールで作成したデータを使って，上の式で係数の a と b を求め，以下のように結果を表示するものとします．

  4. 役に立つ関数 mul

    5. 解答用紙には最初から演算子のモジュールである operator のインポートが入っています．operator モジュールの中にある mul という関数は引数に2つのリストを与えるとその要素どうしの積を返す関数です．これを map 関数と組み合わせることで簡単に Σxi yi を求めることができます．

    使わなくても反復処理で実現できますが．

Student number: s246099

Data generated:
 0.987  1.884 
 2.107  3.767 
 2.973  5.826 
 4.128  7.174 
 4.936 10.123 
 6.040 11.912 
 7.054 14.264 
 8.126 15.861 
 9.186 18.029 
10.136 20.256 

Fitted line: y = -0.323 + 2.018 x

------------------------

計算結果が合っているかは，EXCEL を使って近似曲線を求めることで確認できます．
解答用紙を使用する際には，学生番号と名前の記入も忘れないでください．さらに，解答用紙自体がPythonのプログラムとなっていますので，実行してエラーの無いことを確認してから提出してください．

指定の解答用紙を使用していない，実行時にエラーが出る，学生番号と名前が無い，というような答案は提出されても採点しません．注意してください．

解答例

# #############################
#
# プログラミング入門II 宿題 2025.6.11
# 学生番号：  s246099
# 氏名：     松江 花子
#
# #############################

from make_list import *
from operator import *

print('Student number: s246099')
print()

data = make_list()

print('Data generated:')
for i in range(10):
    for j in range(2):
        print(f'{data[j][i]:6.3f} ', end = '')
    else:
        print()

sum_x = sum(data[0])
sum_x2 = sum(list(map(lambda x: x * x, data[0])))
sum_y = sum(data[1])
sum_xy = sum(list(map(mul, data[0], data[1])))

delta = 10 * sum_x2 - sum_x ** 2
a = (sum_x2 * sum_y - sum_x * sum_xy) / delta
b = (-sum_x * sum_y + 10 * sum_xy) / delta

print()
print(f'Fitted line: y = {a:.3f} + {b:.3f} x')

print('\n------------------------\n')

Back