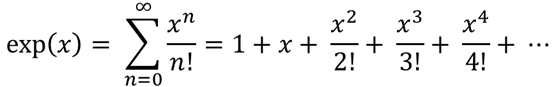
再帰を使って指数関数 exp(x) の値を以下に示す Euler の公式を用いて計算してみましょう.
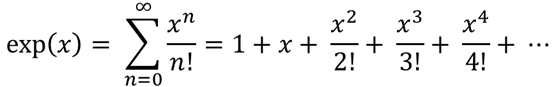
x の値としては乱数により発生させた 5 から 10 までの整数のどれかとします.また,Euler の公式のどの次数 n まで計算するかですが,10 から 50 まで 10 刻みとします.
比較のために使用する実際の exp(x) の値は math モジュールに exp 関数が用意してありますので, math モジュールをインポートしておけば math.exp(x) で計算できます.今回は階乗計算と Euler の式の計算の2つを再帰関数としてください.
Student number: s246099 exp(8) = 2980.9579870417283 Approximation of exp(8) by Euler fomula 10: 2432.12126984127 20: 2980.6778726686925 30: 2980.957985441033 40: 2980.9579870417274 50: 2980.957987041728 ------------------------ |
漸化式を考えるとわかりますが,n 次までの和は n - 1 次までの和とどういう関係にあるかを考えてください.
|
解答用紙を使用する際には,学生番号と名前の記入も忘れないでください.さらに,解答用紙自体がPythonのプログラムとなっていますので,実行してエラーの無いことを確認してから提出してください. 指定の解答用紙を使用していない,実行時にエラーが出る,学生番号と名前が無い,というような答案は提出されても採点しません.注意してください. |
解答例
# #############################
#
# プログラミング入門II 宿題 2025.5.28
# 学生番号: s246099
# 氏名: 松江 花子
#
# #############################
import random
import math
print('Student number: s246099')
print()
def factorial(n):
if n > 0:
return n * factorial(n - 1)
else:
return 1
def euler(n, x):
if n == 0:
return 1
else:
return euler(n - 1, x) + x ** n / factorial(n)
x = random.randint(5, 10)
print(f'exp({x}) = {math.exp(x)}')
print(f'\nApproximation of exp({x}) by Euler fomula')
for n in range(10, 60, 10):
print(f'{n:2}: {euler(n, x)}')
print('\n------------------------\n')
|