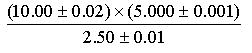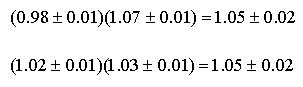より厳密な有効数字の計算方法

　最終結果の小数桁数は小数桁数のもっとも少ない数値に合わせます．したがって，加算と減算の規則はよく使う有効数字の計算方法と同じです．

　例えば33.1±0.1，3.56±0.02，0.592±0.001および1.0894±0.0002の４つの数字を足してみましょう．
合計の不確定さは
　ρ=0.1＋0.02＋0.001＋0.0002=0.1212となります．
最終結果が不確定な数字を1つだけ含むようにするには小数第2位以下を切り捨てて，不確定さを
　ρ=0.1とします．

　したがって，実際の計算は
　33.1+3.56+0.592+1.0894=38.3414を
　38.3と丸めてやればいいことになります．

　各項および最終結果の数字の桁数を整理し，決定するにあたっては，整理後の不確定度の相対値がもとのデータの不確定度の最大相対値を越えることがないようにします．この規則は乗除算においては相対系統誤差が直接，最終結果に伝達されるという事実に基づいています．

例題（定量分析化学:培風館より）
　次の計算を行い，最終結果の不確定度の最大値を求めよ．不確定度を系統誤差として取り扱うものとする．

不確定度の相対値は
　　　　　10.00　　　　2.0ppt
　　　　　5.00　　　　0.2ppt
　　　　　2.50　　　　4.0ppt
合計　　　　　　　　6.2ppt

　すなわち最終結果の不確定度は6.2pptとなります．最終結果20.000･･････を適当に整理して，不確定度の相対値を6.2にします．20.00とすると不確定度は少なくとも±0.01となり，その相対値は0.5pptで実際の値より小さくなります．もし20.0とすると不確定度は少なくとも0.1となり，相対値は5.0pptとなり，合計値6.2に近い値が得られます．20にすると，不確定度は±1となり，相対値は50pptとなり大きすぎます．したがって，20.0とするのがよいことになります．

　このようなルールで有効数字どうしの計算をした場合でも，有効数字桁数が最小のデータの桁数に合わせるというよく使われる有効数字の乗除算の規則とほとんどたいてい一致します．

　この2つの結果の不確定度は同じですが，上の式の0.98の有効数字は2つしかありません．よく使われる方法では上の結果は1.1と表示することになります．厳密には3けたまで有効数字を取るのが正しいということになります．