１．２つ以上の要因について，その効果を考えたい．

　前回の授業では一元配置の分散分析について学びました．一元配置の分散分析では一つだけの要因について，その要因がデータの変動に関与しているかを，データの変動を要因によって変動した部分と偶然誤差による意味のない変動に分けることによって，解析しました．一元配置の分散分析では例えば，餌の種類が羊の成長に及ぼす影響があるのか，あるいは肥料の量が水稲の収量に及ぼす影響があるのかを検出できます．

　今度は，２つ以上の要因について，それらの要因がデータの変動に関与しているかを解析します．例えば，餌の種類に加えて，品種の違いが羊の成長に及ぼす影響があるのか，あるいは肥料の量に加えて，作期の違いが水稲の収量に及ぼす影響があるのかを解析したいとします．

　古典的な方法は一方の要因Ａを固定しておいて，もう一つの要因をｂ変化させ，変化させた要因のｂ最適な水準を決め，次に要因Ｂを固定して，今度は要因Ａの最適な水準を決め，その結果の組み合わせを要因Ａと要因Bの最適な組み合わせとしました．しかしこのやり方には次のような問題があります．

例：ヤギの成長がよくなる薬A，B，C，Dは餌と混ぜて使用する．混ぜる餌の種類によって薬の効果が異なるかもしれないので，麦わら，稲わら，濃厚飼料の３種類と組み合わせて試験したい．

　この試験では要因（処理）は２つあり，薬と餌です．そして，薬は５水準（対照区を含める），餌は３水準あります．比較すべき試験は薬A＋麦わら，薬A＋稲わら，薬A＋濃厚飼料，薬A＋麦わら，薬A＋稲わら，薬A＋濃厚飼料，薬B＋麦わら，薬B＋稲わら，薬B＋濃厚飼料，薬C＋麦わら，薬C＋稲わら，薬C＋濃厚飼料，薬D＋麦わら，薬D＋稲わら，薬D＋濃厚飼料，対照区＋麦わら，対照区＋稲わら，対照区＋濃厚飼料となります．

　古典的な試験法ではまず薬品で一番効果のあるもの（例えば薬C）を，固定した餌（例えば麦わら）で決定し，その後，薬Cを固定して，３つの餌のうちどれがよいかを決めます．しかし，もし麦わらでは薬Cが一番効果があったが，稲わらでは薬Bが最も効果が高かったとしたら，この方法では検出できません．このように２つの要因の絡み合った効果を交互作用といいます．

２．交互作用のいろいろ

　交互作用にはいくつかの種類があります．
A.組み合わせの妙
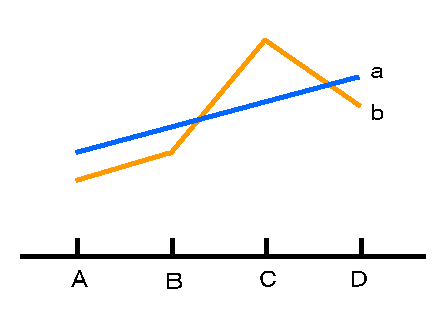
　下の図のようにある特定の組み合わせだと反応が高くなる（あるいは低くなる）ということがおこる場合，交互作用があることになります．下の図ではもし始めにA，B，Dのどれかを固定して，ａとｂを比較したら一番最適な組み合わせであるＣとｂは発見できません．

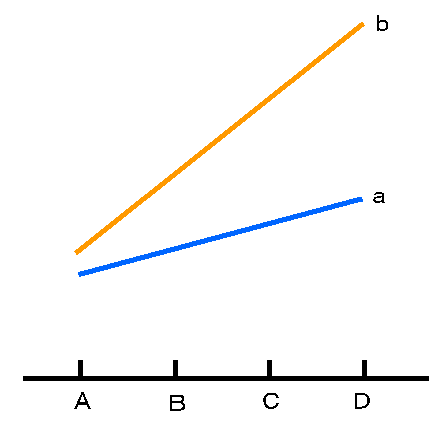
Ｂ．相乗効果
　２つの要因が重なるとより効果が大きくなる場合です．

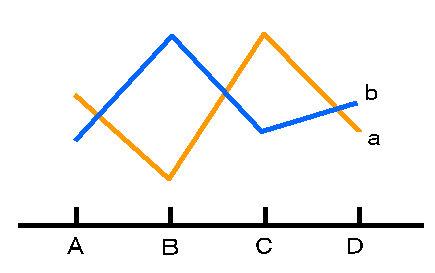
Ｃ．打ち消しあう場合（相殺効果ともいう）
　片方の要因の効果が高いともう一方の要因の効果がうち消す場合です．

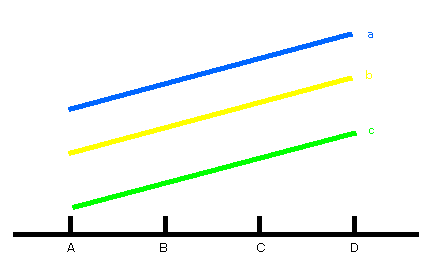
Ｄ．交互作用のない場合
　下のような図になれば，交互作用はありません．しかし，こういうときでも２つの要因を同時に実験する方が，実験の効率がよく，誤差も小さいことがわかっています．

３．二元配置の分散分析
　分散分析ではデータの変動（ばらつき）を偶然誤差による意味のないばらつき（誤差変動）と処理による変動にわけ，誤差変動に対して，処理による変動が十分に大きいかをＦ検定で検定する方法です．したがって，誤差変動をできるだけ小さくすることができれば，Ｆ検定での検出力が高まるはずです．

　要因が２つあるときには，要因Ａ，Ｂとすると

総変動＝要因Ａおよび要因Bによる変動＋誤差変動
　　　　　＝要因Aによる変動＋要因Ｂによる変動＋要因Ａと要因Ｂの交互作用による変動＋誤差変動

以上のようにデータのばらつきを分離することができます．交互作用による変動を分離するには同じ処理の組み合わせについて２つ以上のデータの反復が必要になります．反復のないときは交互作用による変動と誤差変動を分離できません（交絡しているといいます）．

４．二元配置の分散分析
　二元配置の分散分析のやり方は授業で説明します．実際にはパソコンで計算することになりますから，ここではエクセルを使って二元配置の分散分析をする方法を説明します．

５．宿題
Ａ．先週の宿題４．で得たデータについて，繰り返しのある二元配置の分散分析を行え．交互作用のあるときはどのような交互作用があるのか（相乗効果，組み合わせの妙など）をグラフを書くことによって考えよ．さらに交互作用の大きさと主効果の大きさを比較せよ．パソコンで統計解析した場合，使用したソフト名を示し，ワークシートを出力して印刷したものをノートに貼って，提出すること．

Ｂ．第１回の講義でごく簡単にフィッシャーの三原則について説明した．フィッシャーの三原則とは
１．反復，２．無作為化，３．局所管理である．
　局所管理の例として，５品種の水稲について収量を比較する実験を考えてみよう．１つの品種について１反復について20m²の水田が必要であるとしよう．３反復の実験を行うので，20×3×5で300m²の水田が必要となる．300m²の水田が地力ムラのない均一な水田であれば何の問題もないが，現実にはそのような水田はほとんど見つからないであろう．こういうとき反復ごと，すなわち比較した５つの品種が１セット入る水田はなるべく均一になるようにして，100m²のブロックを３つ作る．これが局所管理である．水田の中で，地力の高いところ，中くらいのところ，低いところの３つに分け，それぞれのブロック内では土を混ぜるなどの操作でムラをなるべく減らすようにする．

　さて，このような局所管理は実験のいろいろな場面で要求される．以下の実験では，どのような局所管理が必要かを考えて見よ．
Ａ．何人かのモニターに３種類のレトルトカレーの新製品を試食してもらう．
Ｂ．５種類のガソリンの性能をテストした．ガソリンを別々の車に入れ，一日，所定のコースを走らせ，燃費，排気ガス，その他を調べた．この実験を数日行った．
Ｃ．実験に未熟な３人が，５種類のトマトの酸度について，ビューレットで滴定する方法で調べた．
Ｄ．日当たりのあまりよくない谷間で５品種の柿の収量実験を行う．