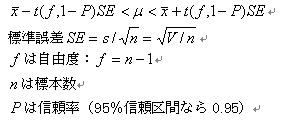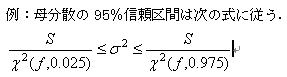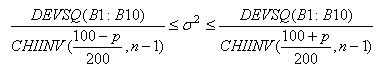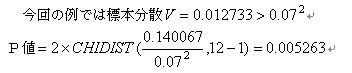��V��@�����z�E�J�C��敪�z
�h��
�P�D��T��̏h��Œ��������f�[�^��p���āC�Q��ނ̗��̏d���̕ꕽ�ς������ł��邩��L�Ӑ���5���ł����肹��D�܂��C���ꂼ��̗��ɂ��āC���̕ꕽ�ς���ѕ�W������95���M����Ԃ����āC���肹��D
�@�Ή��̂Ȃ��Q�̏��W�{�Ɋւ��邔����ł͂Q�̕W�{�̕ꕪ�U�����������Ƃ������Ƃ��ċ��߂��܂��D�Q�̕W�{�̕ꕪ�U���������������肷��̂͂e����łł��܂��D�����Q�̕W�{�̕��U���قȂ�ꍇ��Welch�̌���ɂ���āC�Q�̏��W�{�̕��ς����肵�܂��DWelch�̌���ɂ��Ă͎��Ƃł͐������܂���ł������C�G�N�Z���ł͂����蓯�l�ɊȒP�Ɍ���ł��܂��D
�@�O��̍u�`�ł́C�W�{���\���ɑ傫�����邢�͕ꕪ�U�����m�ł��邱�Ƃ������ɐ��K���z��p���āC���肵�܂����D�������C�W�{�������Ȃ��Ƃ��͕ꕪ�U��W�{�̕��U���琄�肷��덷�����邽�߂ɁC���̕s�m�������������������z�ɂ���āC����E���肵�Ȃ�������܂���D
�R�D������
95���̐M����Ԃŕꕪ�U�𐄒肷��ꍇ�C
�����a���r�C���R�x�����C�T���v���������C�W�{�̕��U���u�Ƃ����
�ꕪ�U���Q�͎��̋�Ԃ�p���̊m���œ���
�T�D�J�C��敪�z���g�������U�̋�Ԑ���
�@�J�C��敪�z�𗘗p����ƁC�W�{���瓾��ꂽ���U�𗘗p���āC�ꕪ�U����Ԑ��肷�邱�Ƃ��ł��܂��D
�S�D�J�C��敪�z
�@�ꕪ�U�����m�̎��ɕW�{�̕��U���ǂ̂悤�ȕ��z����������\���̂��J�C��敪�z�ł��D�J�C��敪�z�͎��R�x�����Ō��肵�C�ꕪ�U�̒l���Q�͊֗^���܂���D
�ȏ�̂��Ƃ���A�������i���U�͕ω����Ȃ������j��1���̗L�Ӑ����Ŋ��p����܂����D���������āC�����b���̕��U�͕ω������ƌ��_�ł��܂����D
�J�C��敪�z��p���āC����W�{�̕��U������l�ł��邩�Ƃ������Ƃ�����ł��܂��D
��F�j�q��̋��̓����b���̕W������0.07%�ł������D�V��������@�̓����œ����b���ɂ�����ω���������m�肽���D12����ׂɒ����������ʂ͈ȉ��̒ʂ�ł���D
7.02,7.03,6.82,7.08,7.13,6.92,6.87,7.02,6.97,7.08,7.19,7.15
�U�D�J�C��敪�z���g�������U�̌���
��Ƃ��āC�����f����`�ŕ����̖@���ɏ]�����f�[�^������ꂽ�������肵�Ă݂悤�D
���R�x���P�̏ꍇ�́C���Q�̒l����⍂�߂ɎZ�o����邽�ߘA����������̂�0.5��(Oi-Ei)��������Ă����悵�܂��D
�V�D�J�C��挟��̉��p
�@�J�C��挟��̓����f����`�̕������C�v���i�䗦�j�f�[�^�̕W�{�i�Q�j�̍��̌���ɂ����p�ł��܂��D�C�G�X�|�m�[�C���|���ȂǓ�ґ���I�ȃf�[�^�ł��邽�ߔ��e�f�[�^�Ƃ��Ă�܂��D���̏ꍇ�ɂ͎��̒l���Z�o���C�J�C���\�ɏƂ炵�Č��肵�܂��D
�A�������F�@�������9:3:3:1�ł���D
�Η������F�@������9:3:3:1�ł͂Ȃ��D
��F�ԐF�ԐF�E���䂪�����~�ԐF���F�E���䂪�Ⴂ����z����F�P�͂��ׂĉԐF�ԐF�E���䂪�����ƂȂ����DF�P���m����z�������ʁC�ȉ��̕\�̂悤�Ȍ��ʂ��D�����9:3:3:1�̕�����ɓK�����邩�����肹��D
| ��`�q�^ |
�\���^ |
�ώ@�lOi |
������ |
���_�lEi |
| �ԁ|���| |
�ԐF�ԐF�E�w�䂪���� |
65 |
9 |
160�~9/16=90 |
| �ԁ|��� |
�ԐF�ԐF�E�w�䂪�Ⴂ |
50 |
3 |
160�~3/16=30 |
| �������| |
�ԐF���F�E�w�䂪���� |
30 |
3 |
160�~3/16=30 |
| ������� |
�ԐF���F�E�w�䂪�Ⴂ |
15 |
1 |
160�~1/16=10 |
| �v |
|
160 |
16 |
�R�D���番�U���͂Ƃ����C�����ɓ���ꂽ�R�ȏ�̕W�{�ɂ��āC���̕�W�c�̕��ςɗL�ӂȈႢ�����邩�����肷����@���w�ԁD���݂Ɏ��̂悤�Ȓ����̂����P��I��Œ������s���C��ԍ��̑傫���Q�̊Ԃł�����������Č���D
�@�@�R�ȏ�̃X�[�p�[�̗�(10�ȏ�����ꂼ�꒲�ׂ�j�ɏd���̈Ⴂ�����邩�H�Ȃ��C�ʂɗ��łȂ��Ă����܂�Ȃ��D
�A�@�R�ȏ�̕i��̃C�l��1��n�Ԑ��i10��ȏ�����ꂼ�꒲�ׂ�j�ɍ������邩�H������ʂɃC�l�̕�Ɍ���Ȃ��D
�B�@�R�ȏ�͔̍|���@���邢�͕i��̈قȂ�ʎ��̓��x���邢�͎_�x�i10�ʈȏ�ɂ��Ă��ꂼ�꒲�ׂ�j�ɍ������邩�H
�P�D�����z
�@�W�{���\���ɑ傫���Ƃ��C���邢�͕ꕪ�U�����m�̂Ƃ��͐��K���z���g���āC�ꕽ�ς���Ԑ��肵����C�ꕽ�ςɊւ��錟����s�����Ƃ��ł��܂��i�O��̍u�`�j�D�������C�W�{�����܂�傫���Ȃ��Ƃ��́C�W�{���U���ꕪ�U�ɓ������Ɖ���ł��Ȃ��Ȃ�܂��D���̂Ƃ��͂����z���g���āC�W�{����ꕽ�ς���Ԑ��肵����C�ꕽ�ςɊւ��錟����s���܂��D
�Q�D�����z�ɂ���Ԑ���
�@�W�{���������Ƃ��ł��_����ł͕W�{���ς����̂܂ܕꕽ�ς̓_����l�Ƃ��܂��D�������C���̓_���肪�ǂꂾ���̌덷���܂�ł��邩�͂���ł͑S���]���ł��܂���D���������āC�M����Ԃ����ċ�Ԑ��肷������悢���Ƃ��킩��܂��D
�@�M�����o�̂Ƃ��̕ꕽ�σʂ̐M����Ԃ͈ȉ��̎���p���Čv�Z�ł��܂��D
�G�N�Z����p���āC�����z�𗘗p�����ꕽ�ς̋�Ԑ����������@�͂Q����܂��D�ЂƂ͐�قǂ̎��𗘗p���āC�v�Z������@�ł��D
�G�N�Z���ł�t(f, 1-P)��TINV(1-P, f)�Ƃ������Ōv�Z�ł��܂��D���������āC�G�N�Z���ł͐M�����o�̂Ƃ��̕ꕽ�σʂ̐M����Ԃ́C
���F�`�����̍�����6�{�̍���ׂɑI�сC�ɂ����Ԃ̐��𐔂����D���ʁC�ȉ��̃f�[�^���D
123,156,168,190,211,234�D�`�����̍��̉Ԃ̐��i�̕ꕽ�ρj��95�������99���M����Ԃ����ċ�Ԑ��肹��D
������̋�Ԑ���̕��@�́C�G�N�Z���̕��̓c�[������{���v�ʂ��g�����@�ł��D�����v�Z����ƈȉ��̒ʂ�ɂȂ�܂��D
�G�N�Z���Ōv�Z����ꍇ�͈ȉ��̒ʂ�ɂȂ�܂��D
�P�D�A�������ƑΗ������̐ݒ�
�Q�DP�l�̌v�Z
�@�A�����������藧�Ƃ�����C����̕W�{��������m���ł���P�l�̓G�N�Z���ł͈ȉ��̎��Ōv�Z���܂��D
�@���R�x��1�ł���C����Čv�Z����K�v�̂���Ƃ��͈ȉ��̂悤�ɂ��āC�G�N�Z���Ōv�Z���܂��D
�Q�D��T��̏h��Œ��������f�[�^�ɂ��āC����Ԃ����O��̏h��̍u�]�̍Ō�ɏ����Ă���ꕽ�ςȂ�тɕꕪ�U�ɂ��Ă̌�����s���D