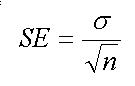第5回 統計的推定
3.標本平均の分布
統計的推測のために母集団から抽出した標本数nの標本から求めた標本平均の分布は次の性質を持ちます.
- 標本平均の期待値は母平均μに等しい.
- 標本平均の分散は母分散の1/nに等しい.
- nが十分に大きいときは大きさnの標本の標本平均は正規分布に近似できる.
統計的解析においては,たいてい母集団の平均を推測するために,標本を集めるのがほとんどですからこのような標本平均の分布は特に重要です.母集団がたとえ正規分布にかなりはずれた分布をしていても平均について論ずるならば,ある程度の数の標本を集めれば,標本平均は正規分布に近似できます.
4.統計的推定
1) 点推定 1つの値で母数を推定します.
例: 朝酌川で無作為に数地点を選び,鯉を釣った.鯉の体重の標本平均は5.0kgなので,朝酌川の鯉の平均体重を5.0kgと推定した.
2) 区間推定 母数をある幅を持つ信頼区間とともに推定します.
例:朝酌川で無作為に数地点選び,鯉を釣った.サンプル数100匹の鯉の体重の標本平均5.0kg,標準偏差2.0kgなので,朝酌川の鯉の平均体重は95%の信頼区間をつけて,5±0.39kgと推定した.このとき,母集団(朝酌川のすべての鯉)の母平均μは95%の確率で4.61<μ<5.39kgの範囲にはいる.
信頼率は統計量を使用する目的に応じて決定します.95%信頼区間の場合,100回のうち5回,区間推定の値に母集団の平均が含まれない(すなわち推定を誤る)ということが起こります.信頼率を高める,例えば100%にしたらよいのではと考える人もいるかもしれませんが,そのときには信頼区間はきわめて大きくなり,役に立たなくなります.例えば,視聴率の100%信頼区間は0〜100%だというようなもので,疑いはできませんが,この数値では何の役にも立ちません.信頼率は必要に応じて設定します.
2.標本平均の分布
私たちが母集団について何らかの性質を知りたいために,その中から無作為に標本を抽出します.たいていまず第一に知りたいことは母集団の平均(母平均)です.では標本の平均と母集団の平均にはどのような関係があるのでしょうか?
ある母集団について,標本を5つ無作為に抽出するという試行を2000回繰り返してみました.
下がその一例です.なおこのシミュレーションは講談社ブルーバックスB-1403
パソコンで遊ぶ数学実験 涌井良幸・涌井貞美著についているCD-ROMのプログラム(No.14)によって行いました.
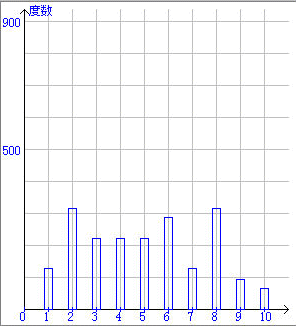
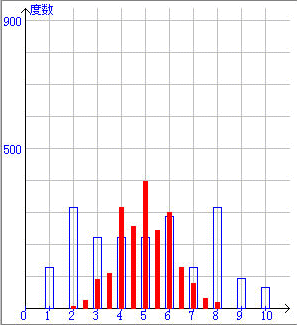
上左の図が母集団の分布を示します.この母集団から5つの標本を無作為に抽出し,その平均をとります.この試行を2000回繰り返し,得られた標本の平均の分布を示したのが,上右の図です.
さて,標本平均の分布は母集団の分布の形に依存するでしょうか?いろいろな母集団について同じ実験をしたら,次のような結果を得ました.
この結果から,どのような母集団であっても,標本平均の分布については以下のことがいえそうです.
1) 標本平均の分布の平均は母集団の平均とほぼ同じになることが多い.
2) 標本平均の分布は正規分布に近い形をしている.
さて,標本を取る数を5個よりも多くすると,標本平均の分布はどうなるでしょうか?同じようにシミュレーションしてみました.
この結果から,どのような母集団であっても,標本平均の分布については以下のことがいえそうです.
3) 標本の数を増やすと標本平均の分布のばらつきが小さくなる.
しかし,標本平均だけをつかって,母集団の母平均を点推定した場合,その推定がどの程度信頼できるのかがわかりません.例えば,試験の成績の母集団において,母平均がほぼ50点,母標準偏差ほぼ15点であるときに5つの標本から母平均を点推定したらどうなるでしょうか?
1.第1回の宿題および第3回の宿題3.で調べたデータについて標準誤差を求めよましょう.このとき第1回の宿題の標準誤差の計算はエクセルの関数を使い,第3回の宿題の標準誤差の計算は分析ツールを使って計算しましょう.次に母集団の母平均を90%信頼区間,95%信頼区間および99%信頼区間をつけて,区間推定しましょう.
このような標本平均の性質から標本平均が母平均を推定するための目安として,標準誤差を計算することができます.標準誤差SEとは標本平均の標準偏差のことです.母集団の標準偏差をσとすると
標準誤差はエクセルでは以下のリンクに載せた方法で計算することができます.
全く実力の同じ者が勝負をすれば,勝つ確率は2分の1であるといえます.逆に実力が違えば,勝つ確率はその実力差に応じて変わると考えられます.このときn回勝負したときに,x回勝つ確率は二項分布に従うと見なせます.
2人で行う勝負(じゃんけん,将棋,相撲なんでもよい)を20回以上行いましょう.もし実力が同じだとした場合,その結果の得られる確率を求めましょう.その確率から,両者の実力に差があるのか,ないのかを考えて見ましょう.(2人1組の班で調査してもかまいません.相手がコンピューターでもかまいません)
なおじゃんけんのような場合では勝つ確率を2分の1として考えてください.(あいこは決着がつくまですることによって勘定しないことにします.)
2.次回の授業ではあるデータが正規分布あるいは二項分布に基づくと仮定して,統計的に推定あるいは検定を行います.例えば,平均m,標準偏差σの正規分布では平均から3σ以上離れた値の出現する確率は0.3%しかありません.このことから逆にそのような値が得られたら,元の平均と標準偏差が怪しいと考えることもできるでしょう.このような考え方を統計的検定といいます.今回は次の実験を行いましょう.
統計的推論には統計的推定と統計的検定の2つがあります.
推定:統計的に標本の統計量から母集団の母数を推測することを統計的推定といいます.
例: 視聴率調査を200人に対して行い,番組Aの視聴率を推定した.
検定:統計的に標本の統計量から母集団の母数に関する予想の真偽を検証することを統計的検定といいます.したがって,イエスかノーかを判定することになります.
例: 視聴率調査を200人に対して行い,番組Aの視聴率が20%以上あるのかを検定した.
例: A社とB社の車の排気ガスに含まれる窒素酸化物はA社の方が多いのかを検定した.
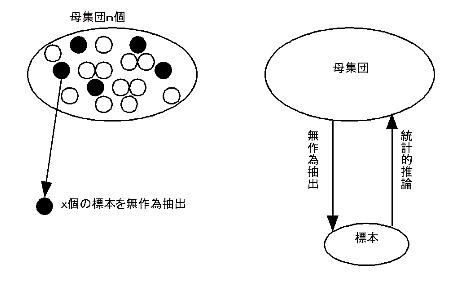
わたしたちはふつう統計データを集めるのは,データを集めた標本そのものに関心があるのではなく,標本をそこから無作為抽出した母集団について何か知りたいから,標本を取り出し,データをとります.わたしたちは母集団そのものについては完全に知ることはいろいろな事情で不可能ですが,標本については具体的なデータ(統計量)を得ることができます.さて,この標本の統計量から母集団の母数を推論できるのでしょうか?そしてどのようにして・・・