第4回 二項分布・ポアソン分布・正規分布
3.正規分布
正規分布は自然界で起こる現象の多くがその分布に当てはまること,特に平均値に関する分布が当てはまることから,統計学では最も重要な分布となっています.
それではまず,正規分布の特徴を以下に列記します.
平均μ,分散σ2の正規分布はN(μ,σ2)と表記され,以下のことがいえます.
- 平均μを中心にして,左右対称である.すなわち平均とメジアンは一致する.そして,平均より大きい値あるいは小さい値を取る確率はどちらも1/2である.
- 曲線は平均μの近傍で高く,両側に行くにしたがって単調に低くなる.
- 平均μは曲線の位置を決める.平均μのみ異なる2つの曲線は左右に移動させれば重ねることができる.(参考図)
- 標準偏差σは曲線の形を決める.σが大きければ曲線は扁平になる.(参考図)
- μ-σとμ+σの間の確率変数を取る確率は約0.68である.(参考図)
- μ-2σとμ+2σの間の確率変数を取る確率は約0.95である.(参考図)
- μ-3σとμ+3σの間の確率変数を取る確率は約0.997である.(参考図)
- 0.95(95%)の確率でμ-1.96σとμ+1.96σの間の確率変数をとる.(参考図)
- 0.99(99%)の確率でμ-2.576σとμ+2.576σの間の確率変数をとる.
正規分布の特徴を具体的に考えてみましょう.20~24歳の男性の身長は人間生活工学研究センターの調査(1992-1994)によると,平均(μ)170.5cm,標準偏差(σ)5.9cmでした.身長の分布が正規分布に従うとしますと,このことから2σ以上平均より背の高い人,すなわち182.3cm以上の人は全体の2.2%になります.平均から標準偏差以内,すなわち164.6~176.4cmに全体の68%が属します.全体の95%は158.9~182.1cmに属します.
3.第3回の宿題で調べたデータについて,そのデータが正規分布で近似できると仮定した場合,第3回の宿題採点表で指定した範囲に属するデータが全体の何パーセントになるかをエクセルのNORMDIST関数を用いて,計算しましょう.
2.ある分布を正規分布とみなしてよいかを判断するには,厳密にはコルモゴロフ・スミルノフの検定を用います.しかし,ここでは第3回の授業の宿題で調べたデータについて,正規分布で予想される分布とどの程度離れているのかを以下の手順で検討してみましょう.
a.調査したデータの標本平均,標本分散をそれぞれ母平均,母分散とする正規分布とすると,68.3%の確率変数はμ-σ~μ+σの間に入ります.自分の調べたデータのうち,何%が実際にはμ-σからμ+σの間に入るかを数えて,調べてみましょう.
b.さらにμ-2σ~μ+2σ,μ-3σ~μ+3σの間に入るデータについても数えましょう.
c.a.,b.の結果から,自分の調査したデータが正規分布に近いかを検討しましょう.
b. a.で求めた確率分布のヒストグラムの上に,先週,調べたデータから作ったヒストグラムをトレーシングペーパーなどで書き写したものを,縦軸,横軸の大きさがそろうように重ねて(パーセント表示に書き換えるなどするとよいでしょう).2つの違いを検討しましょう.もし,大きく異なるときはなぜかを考えてみましょう.
a. それぞれ二項分布,ポアソン分布に従っているとして,確率分布を求めましょう.なおポアソン分布の計算で用いる母平均μは調査したデータの平均を用いたらよいです.
宿題
1.第2回の宿題で調べたデータについてa.は二項分布,b.はポアソン分布で予想される分布とどの程度離れているかを以下の手順で検討しましょう.
1.二項分布
大きさnの標本で,事象Eの起こる確率をpとするとき,そのうちx個にEが起こる確率P(x)は二項分布に従います.
例としては,さいころを10回振ったときに1がx回出る確率分布は二項分布に従います.この場合,大きさn=10,確率p=1/6となります.
二項分布では,母平均μ=np,母分散σ2=np(1-p)となります.
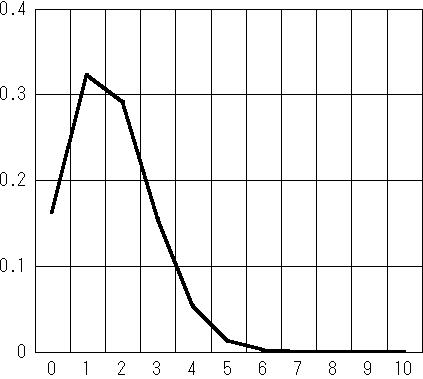
二項分布の具体的な例として,さいころを10回振って,1の出る回数xの確率分布を考えましょう.下の図表のようになります.
| 1の出る回数 |
二項分布に基づく確率 |
| 0 |
0.16 |
| 1 |
0.32 |
| 2 |
0.29 |
| 3 |
0.16 |
| 4 |
0.05 |
| 5 |
0.01 |
| 6 |
0.00 |
| 7 |
0.00 |
| 8 |
0.00 |
| 9 |
0.00 |
| 10 |
0.00 |
以上の二項分布の計算はエクセルを使うと簡単にできます.
2.ポアソン分布
母平均μが与えられたときに事象がx回出現する確率を表すポアソン分布をエクセルで計算する式は以下の通りです.
ポアソン分布では母平均μ=母分散σ2です.
例:ある島では毎年,何千羽ものヒナが生まれます.毎年平均0.5羽の出現率で黄金色の羽をもつヒナが生まれるといいます. ですから,黄金の羽を持つヒナが0,1,2羽,出現する確率はそれぞれポアソン分布に従うということができます.(ここでは毎年それぞれ誕生するヒナの数が何千羽であるかを正確にわかっていなくてもよいし,異なっていたとしてもよいです.そこが二項分布と違うところです.)
正規分布はかなり難しい数式で表現されます.しかし,エクセルでは正規分布に関する関数がいくつかあるので,数式を知らなくても正規分布に関する計算を,エクセルを使って,することができます.
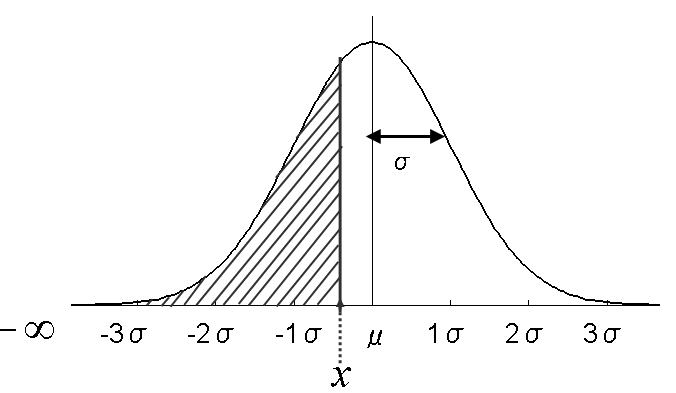
平均がμ,標準偏差がσである正規分布において,x以下の範囲に属する割合を
NORMDIST(x, μ, σ, true)で計算します.下の図の斜線の割合を求める関数です.
エクセルにおける正規分布の計算の詳細は以下をクリックしてください.
4.次回以降の授業ではあるデータが正規分布あるいは二項分布に基づくと仮定して,統計学的に推定あるいは検定を行います.次回の授業では統計的な推定について考えます.統計的な推定とは,母集団についてのある数値を知るために,母集団から無作為抽出した標本からデータを集め,そこから母集団についてのある数値を推測することです.統計的な推定の例を以下にいくつかあげます.
A.20歳代の男女を100人,無作為抽出して,1ヶ月の携帯電話代を調べたところ,平均5000円,標準偏差500円だった.母集団(20歳代の男女すべて)の携帯電話代はいくらかを推定したい.
B.A農場はBスーパーにトマトを納入している.Bスーパーは仕分けの手間を省くためにトマトの重さの標準偏差を1g以内にすることを求めてきた.すべてのトマトの重さを測定できないので,100個を無作為抽出して標準偏差を調べたところ,0.99gだった.A農場のトマト全体の重さの標準偏差はいくらと推定できるだろうか?
C.C林業はD山を開発しようと考えたが,開発の利益に出費が見合うかわからない.D山の樹木すべてを調べることは不可能なので,無作為に数地点を選んで樹木の価値を算定し,D山全体の樹木の価値を推定した.
以上のような例に当てはまる事例をいくつか考えてみましょう.
さいころを10回振ったときに1が0回出る(x=0)確率は,P(0)=0.162である.
さいころを10回振ったときに1が3回出る(x=3)確率は, P(3)=0.155である.
ポアソン分布,正規分布は二項分布から導き出せるので,二項分布がどんなものかを詳しく知るとよりよくポアソン分布,正規分布を理解できるでしょう.
3.二項分布とポアソン分布の正規分布での近似
計算機の発達していない時代では二項分布とポアソン分布の計算はかなり面倒でした.いまでもnの大きい二項分布は正規分布に近似した方がよい場合もあるかもしれません(あまりに大きい階乗を計算するとエラーになることもあるし,桁落ちして誤差が大きくなりやすいので).しかし,たいていの用途ではパソコンで統計解析するときには,二項分布やポアソン分布のままで計算できるでしょう.
母平均μが与えられたときに事象がx回出現する確率を表すポアソン分布の一般式は以下の通りです.
ポアソン分布は二項分布において平均npを一定にして,nを無限大にすると得られます.すなわち確率pはきわめて小さい値ということになります.確率・統計入門(小針晛宏,岩波書店)のP63(ポアソン分布)に照明があります.
ポアソン分布は一定の長さの時間,一定の大きさの空間においてごくまれに起こる事象を表現するときに用います.二項分布において平均μ=npを一定にし,pをどんどん小さくする一方で,
nを無限大にすると得られます.非常に大きな集団においてきわめて起こりにくい事象を対象としたときの分布です.
二項分布と違って,分布の大きさnは必要ありません.例えば,交通事故死はきわめてまれなものです.その対象となるnはしかも何人か決めようがありません.運転者や歩行者の数は毎日異なるからです.そういうときにポアソン分布は有効です.