戞侾俀夞丂憡娭暘愅
侾丏俀偮偺曄検娫偺娭學傪挷傋傞
丂愛庢僇儘儕乕偲寣埑偺娭學丆擭暯嬒婥壏偲擭娫崀悈検丆擔幩検偲僐儉僊偺廂検側偳俀偮偺曄悢娫偺娭學傪挷傋傞偙偲偼昿斏偵偁傝傑偡丏偙偺応崌丆傑偢嶶晍恾傪彂偔偙偲偐傜巒傔傑偡丏嶶晍恾傪彂偔堄媊偼埲壓偺俁偮偑偁傝傑偡丏
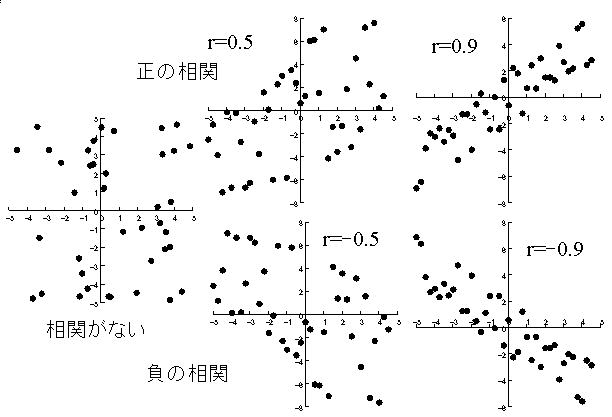
- 帇妎揑偵偳傫側娭學偐傪峫偊傞偙偲偑偱偒傞丏俀偮偺曄悢娫偺娭學偼捈慄偱昞偣傞偙偲傕偁傟偽丆嬋慄乮俀師娭悢丆巜悢娭悢丆懳悢娭悢側偳乯偱昞偣傞偙偲傕偁傝傑偡丏悢帤偩偗偱偼偳偺傛偆側娭學偐偼傢偐傝偵偔偄応崌偱傕丆僌儔僼偵偡傞偲堦栚偱傢偐傝傑偡丏
- 堎忢抣偺敪尒偑偱偒傞丏
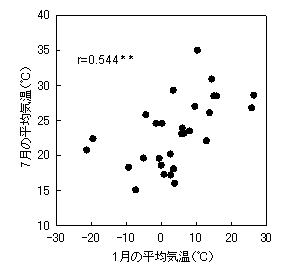
- 僨乕僞偺廤抍傪堎側傞僌儖乕僾偵暘偗傜傟傞偙偲偑偁傞丏愛庢僇儘儕乕偲寣埑偺娭學偑惈暿丆怑嬈偦偺懠偄傠偄傠側梫場偵傛偭偰曄傢傞偙偲傕偁傝傑偡丏偦偺応崌偱傕僌儔僼偵偟偰斾妑偡傟偽怴偟偄梫場傪敪尒偱偒傞偙偲偑偁傝傑偡丏椺偊偽壓偺侾寧偺婥壏偲俈寧偺婥壏偺椺傪僋儕僢僋偟偰偔偩偝偄丏
丂嶶晍恾偼僄僋僙儖偱傕娙扨偵彂偗傑偡丏
俀丏憡娭偲夞婣
丂俀偮偺曄検乮倶丆倷乯偺娭學偵偮偄偰丆倶丆倷偲傕偵惓婯暘晍偵偟偨偑偭偰偽傜偮偔検偱偁傞偲偒偵偼椉幰偺娭學傪憡娭暘愅偟傑偡丏堦曽丆倶偵偮偄偰偼巜掕偱偒傞曄悢乮撈棫曄悢乯偱偁傝丆倷偑巜掕偝傟偨倶偵懳偟偰偁傞偽傜偮偒傪傕偭偰寛傑傞応崌丆倶偲倷偺娭學傪夞婣暘愅偟傑偡丏
丂憡娭暘愅偱偼椉曄悢娫偺娭楢偺搙崌偄傪憡娭學悢偱昡壙偡傞偙偲傪庡側栚揑偲偟傑偡丏夞婣偱偼憡娭學悢偱昡壙偡傞偙偲傕偱偒傑偡偑丆庡偨傞栚揑偼椉曄悢娫偺悢揑娭學傪夞婣捈慄偱昞偟丆偁傞倶偑巜掕偝傟偨偲偒偵倷偑偄偔偮偵側傞偐傪媮傔傞乮悇掕偁傞偄偼梊應偡傞乯偙偲偱偡丏
俁丏憡娭暘愅
1) 憡娭暘愅偺庤弴
丂憡娭暘愅偱偼師偺庤弴偱摑寁揑側夝愅傪峴偄傑偡丏
- 憡娭學悢傪媮傔傞丏
- 曣憡娭學悢兿亖侽偲偄偆婣柍壖愢傪専掕偟丆憡娭學悢偑桳堄偱偁傞偐乮俀偮偺曄悢娫偵憡娭偑偁傞偐乯傪専掕偡傞丏
- 昁梫偱偁傟偽丆曣憡娭學悢偺嬫娫悇掕傪峴偆丏
- 憡娭學悢偑桳堄偱偁傟偽丆偦偺愨懳抣偺戝偒偝偐傜憡娭偺嫮偝傪昡壙偡傞丏
- 椉曄悢偺場壥娭學側偳傪愱栧揑側抦幆側偳傪摦堳偟偰丆偝傜偵夝愅偡傞丏
丂僄僋僙儖傪巊偭偰丆憡娭學悢傪寁嶼偡傞偙偲偑偱偒傑偡丏
俇丏廻戣
俙丏帺暘偺挷傋偨俀偮偺曄検偺娫偺娭學偵偮偄偰丆椉曽偺僨乕僞偲傕偵偄偐偺乮侾乯乣乮俁乯傑偱傪峴偊丏
乮侾乯丂嶶晍恾傪彂偔忋偱偺拲堄偵偟偨偑偭偰丆嶶晍恾傪彂偒捈偣丏
乮俀乯丂95亾怣棅嬫娫傪偮偗偰曣憡娭學悢傪嬫娫悇掕偣傛丏
乮俁乯丂憡娭偺桳柍乮婣柍壖愢兿亖侽乯傪専掕偣傛丏
俛丏帺暘偺挷傋偨憡娭偵偮偄偰偺僨乕僞偵憡娭偑偁傞偲偒偼偳偆偄偆娭學偑偁傞偐傪峫偊傛丏偡側傢偪傒偐偗偺憡娭偱偼側偄偺偐丆捈愙揑側場壥娭學偑偁傞偺偐丆偁傞偄偼壗偐暿偺梫場偑娫偵偼偄偭偰偄側偄偐丠憡娭偑側偄偲偒偼乮巒傔憡娭偑偁傞偲梊憐偟偨偵傕偐偐傢傜偢丆乯側偤憡娭偑側偐偭偨偺偐傪峫偊傛丏
2) 憡娭學悢 倰
丂俀偮偺曄悢娫偺捈慄揑側娭學乮憡娭娭學乯偼憡娭學悢倰 偵傛偭偰掕検揑偵帵偡偙偲偑偱偒傑偡丏
丂憡娭學悢偵偼埲壓偺惈幙偑偁傝傑偡丏
丂嘆丂 亅侾亝倰亝侾偱偁傞丏
丂嘇丂 倰偑1偵嬤偄傎偳惓偺憡娭偑嫮偔丆-1偵嬤偄傎偳晧偺憡娭偑嫮偄丏
丂嘊丂 倰偑0偵嬤偄偲偒偼丆椉曄悢娫偵偼憡娭偑側偄乮柍憡娭乯丏
係丏憡娭學悢偵娭偡傞悇掕偲専掕
侾乯丂悇掕
丂憡娭學悢倰偼廤傔偰偒偨僨乕僞乮昗杮乯偐傜媮傔偨傕偺偱偡偐傜丆摑寁検偱偡丏曣廤抍偺憡娭學悢偱偁傞曣憡娭學悢兿傪倰偐傜嬫娫悇掕偡傞偙偲偑偱偒傑偡丏
丂偦偺慜偵曣憡娭學悢兿偑梌偊傜傟偨偲偒偵丆昗杮偺憡娭學悢倰偼偳偺傛偆偵暘晍偡傞偐傪傒偰傒傑偟傚偆丏
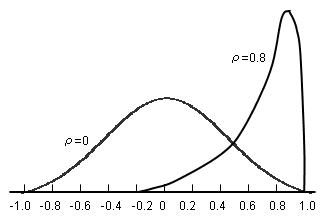
丂壓偺恾偺傛偆偵曣憡娭學悢兿偑0偱偁傞偲偒偵偼丆偦偺曣廤抍偐傜柍嶌堊偵拪弌偟偨昗杮偺憡娭學悢偼嵍塃懳徧偵暘晍偟傑偡丏偟偐偟丆曣憡娭學悢偑亇1偵嬤偯偔偲挊偟偔備偑傫偩暘晍傪偟傑偡丏
偙偺娭學傪棙梡偟偰丆昗杮偺憡娭學悢 偑摼傜傟偨偲偒偵曣憡娭學悢傪嬫娫悇掕偱偒傑偡丏
丂怣棅棪傪99亾傑偨偼90亾偲偟偨偗傟偽丆庤弴俀偺幃偺1.960傪2.576傑偨偼1.645偲曄峏偟傑偡丏
丂僄僋僙儖傪巊偭偰曣憡娭學悢偺嬫娫悇掕傪偡傞偲偒偼埲壓偺曽朄傪嶲峫偵偟偰偔偩偝偄丏
俀乯丂専掕
丂曣憡娭學悢兿偵娭偡傞専掕偼丆偨偄偰偄偺応崌丆婣柍壖愢俫侽丗兿亖0丆懳棫壖愢俫侾丗兿亗0偲偡傞柍憡娭偺専掕偱偡乮俀偮偺曄悢娫偵憡娭偑側偄偲偄偆婣柍壖愢傪専掕偟傑偡乯丏
婣柍壖愢丗椉曄悢娫偵偼憡娭偑側偄丏曣憡娭學悢兿亖0
懳棫壖愢丗椉曄悢娫偵偼憡娭偑偁傞丏曣憡娭學悢兿亗0
婣柍壖愢偑婞媝偝傟偨偲偒偼椉曄悢娫偵偼憡娭偑偁傞偲寢榑偱偒傑偡丏
婣柍壖愢偑婞媝偱偒側偐偭偨偲偒偼椉曄悢娫偵偼憡娭偑偁傞偲偼偄偊側偄偲寢榑偱偒傑偡丏
曣廤抍偺曣憡娭學悢兿亖0偺偲偒偱傕丆偦偙偐傜柍嶌堊偵庢傝弌偟偨昗杮偺憡娭學悢偑0.5掱搙偺偐側傝戝偒側抣偲側傞偙偲傕傛偔偁傝傑偡偐傜丆憡娭學悢倰傪寁嶼偟偨偩偗偱憡娭偺桳柍傪敾抐偟偰偼偄偗傑偣傫丏
忋偺椺戣傪僄僋僙儖偱寁嶼偡傞偲偒偼壓偺傛偆偵偟傑偡丏
俁乯丂憡娭偺嫮偝
丂憡娭學悢 偺専掕偺寢壥丆憡娭偑桳堄偱偁傞偙偲偑傢偐偭偨傜丆憡娭帺懱偺嫮偝偼憡娭學悢偺愨懳抣偱敾抐偟傑偡丏偍偍傓偹師偺傛偆偵峫偊傑偡丏
丂丂丂-1.000乣-0.600丂崅偄晧偺憡娭
丂丂丂-0.599乣-0.400丂拞埵偺晧偺憡娭
丂丂丂-0.399乣-0.200丂掅偄晧偺憡娭
丂丂丂-0.199乣+0.199丂柍憡娭
丂丂丂+0.200乣+0.399丂掅偄惓偺憡娭
丂丂丂+0.400乣+0.599丂拞埵偺惓偺憡娭
丂丂丂+0.600乣+1.000丂崅偄惓偺憡娭
丂偟偨偑偭偰丆憡娭學悢偑1亾偁傞偄偼偦傟傛傝彫偝偄桳堄悈弨偱桳堄偱偁偭偨偲偟偰傕丆憡娭學悢帺懱偺抣偑0偵嬤偗傟偽丆俀偮偺曄悢娫偺憡娭偼偁傑傝戝偒偄偲偼偄偊傑偣傫丏昗杮悢偑懡偔側傞偲丆憡娭學悢偑偐側傝0偵嬤偔偰傕桳堄偵偼側傞偺偱丆偙偺揰偵拲堄偟傑偟傚偆丏
丂榑暥側偳偱憡娭學悢偵*傗**偑晅偄偰偄傞偙偲傪傛偔尒傑偡丏偙傟偼丆曣憡娭學悢偑0偱側偄偙偲傪専掕偟偰偄傑偡丏傆偮偆*偼5亾偺桳堄悈弨偱憡娭偑偁傞偲偒丆**偼1亾偺桳堄悈弨偱憡娭偑偁傞偙偲傪帵偟偰偄傑偡丏
俆丏傒偐偗偺乮婾偺乯憡娭娭學
丂憡娭學悢偑崅偄偐傜偲偄偭偰丆椉幰偺娫偵場壥娭學側偳偑昁偢偁傞偲偼尷傝傑偣傫丏椺偊偽丆擭楊傪栤傢偢偵挷嵏偟偨傜丆寣埑偲悅捈旘傃偵晧偺憡娭娭學偑偁傞偐傕偟傟傑偣傫丏偟偐偟丆壛楊偲偲傕偵寣埑偼忋偑傝丆塣摦擻椡偼棊偪傞偐傜丆偙偺娭學偼尒偐偗偺傕偺偱偟偐偁傝傑偣傫丏偁傞偄偼僥儗價偺晛媦棪偲暷偺徚旓検傪1960擭戙偵偮偄偰挷傋偨傜丆晧偺憡娭偑偁傞偱偟傚偆丏堦斒偵帪娫偺棈傓僨乕僞偱偼尒偐偗偺憡娭娭學偺弌偰偔傞偙偲偑傛偔偁傝傑偡丏
侾乯丂帪宯楍僨乕僞
丂1955擭偐傜1970擭偵偍偗傞僥儗價偺斕攧悢偲帺摦幵帠屘偺悢
丂1930擭偐傜1970擭偵偍偗傞僞僶僐偺徚旓杮悢偲暯嬒庻柦
丂埲忋偺偙偲傪挷傋傞偲偳偆偄偆寢壥偑摼傜傟傞偱偟傚偆偐丠
丂偦偺寢壥偐傜丆偳偆偄偆岆偭偨寢榑偑堷偒弌偣傞偱偟傚偆偐丠
俀乯丂擭楊側偳偵娭傢傞僨乕僞
丂寣埑偲尨廻偁傞偄偼憙姏偱梀傇帪娫傪挷傋偨傜偳偆側傞偱偟傚偆偐丠