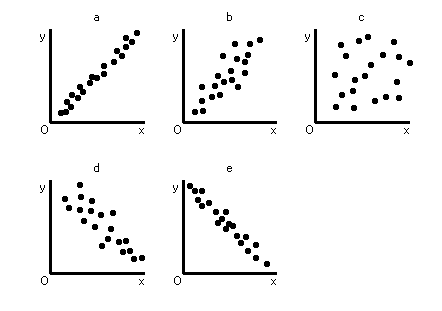戞侾侾夞丂暘嶶暘愅偦偺係丂懡尦攝抲
丂偙偺傛偆偵儔僥儞曽奿朄偵偡傞偲俉偮偺慻傒崌傢偣偑偁偭偨幚尡傪係偮偺張棟偺慻傒崌傢偣偵尭傜偡偙偲偑偱偒傑偡丏偟偐偟丆偙偺応崌丆岎屳嶌梡偼専弌偱偒傑偣傫丏
| 儕儞巁 拏慺 |
俹侽 |
俹侾 |
| 俶侽 |
俲侽丆俲侾 |
俲侽丆俲侾 |
| 俶侾 |
俲侽丆俲侾 |
俲侽丆俲侾 |
丂儔僥儞曽奿朄偵廬偄丆埲壓偺傛偆偵慻傓偲偳偺張棟傕俀夞偢偮尰傟傑偡
乮俲侽亖俙丆俲侾亖俛偲傒側偟傑偡乯丏
| 儕儞巁 拏慺 |
俹侽 |
俹侾 |
| 俶侽 |
俲侽 |
俲侾 |
| 俶侾 |
俲侾 |
俲侽 |
丂儔僥儞曽奿朄偵傛傞堦晹幚巤偺嬶懱椺偲偟偰俁張棟俀悈弨偺幚尡傪峫偊傑偟傚偆丏
丂悈堫偺巤旍幚尡偺椺偱偡丏
丂拏慺乮柍巤旍俶侽丒巤旍俶侾乯丆儕儞巁乮柍巤旍俹侽丒巤旍俹侾乯丆僇儕乮柍巤旍俲侽丒巤旍俲侾乯偺俁張棟傪慻傒崌傢偣偨俉偮偺幚尡傪曓応偺娭學偐傜係偮偺幚尡偵尭傜偟偨偄偲偟傑偡丏
丂傑偲傕偵偡傋偰偺慻傒崌傢偣偵偮偄偰幚尡偡傞偲
俀丏儔僥儞曽奿朄偵傛傞堦晹幚巤
丂偝偰丆懡偔偺場巕傪庢傝忋偘傞偲壗偑傢偐傞偺偱偟傚偆偐丏偦傟偼俁偮埲忋偺場巕偺棈傓岎屳嶌梡偱偡丏偨偲偊偽俙丆俛丆俠丆俢丆俤偺俆偮偺場巕偵偮偄偰幚尡偡傞偲偡傟偽丆俙丆俛丆俠丆俢丆俤偺俆偮偺場巕偺庡岠壥丆俙亊俛丆俙亊俠丆俙亊俢丆俙亊俤丆俛亊俠丆俛亊俢丆俛亊俤丆俠亊俢丆俠亊俤丆俢亊俤偲偄偆俀偮偺場巕娫偺岎屳嶌梡丆俙亊俛亊俠丆俙亊俛亊俢丆俙亊俛亊俤丆俙亊俠亊俢丆俙亊俠亊俤丆俙亊俢亊俤丆俛亊俠亊俢丆俛亊俠亊俤丆俛亊俢亊俤丆俠亊俢亊俤偲偄偆俁偮偺場巕娫偺岎屳嶌梡丆俙亊俛亊俠亊俢丆俙亊俛亊俠亊俤丆俙亊俛亊俢亊俤丆俙亊俠亊俢亊俤丆俛亊俠亊俢亊俤偲偄偆係偮偺場巕娫偺岎屳嶌梡丆俙亊俛亊俠亊俢亊俤偲偄偆俆偮偺場巕娫偺岎屳嶌梡偑傢偐傝傑偡丏偟偐偟丆俁偮埲忋偺場巕偺娭學偡傞岎屳嶌梡偼偦偺夝庍偑擄偟偄忋偵丆傎偲傫偳偺応崌偁傑傝戝偒偔側偄偺偱丆偨偄偰偄偺応崌丆柍帇偟偰傕偐傑傢側偄偙偲偑傢偐偭偰偄傑偡丏
丂奺場巕偺悈弨偑俀偮偺応崌丆庡岠壥偲岎屳嶌梡偺偦傟偧傟偵侾偮偢偮帺桼搙偑妱傝摉偰傜傟傞偺偱丆庡岠壥偲俀偮偺場巕娫偺岎屳嶌梡偺帺桼搙偺崌寁偼15丆幚尡慡懱偺帺桼搙偼31側偺偱丆俆偮偺場巕傪俀悈弨偡傋偰幚尡偡傞偲丆崌寁32偺幚尡偑嵟掅偱傕昁梫偱偡偑丆庡岠壥偲俀偮偺場巕娫偺岎屳嶌梡偵尷掕偟偨傜丆敿暘偺16偺幚尡傪偡傟偽傛偄偙偲偵側傝傑偡丏
丂偙偺傛偆偵幚尡偺悢傪尭傜偟丆偟偐傕偱偒傞偩偗惛搙傪壓偘偢丆傑偨丆抦傞傋偒岎屳嶌梡乮俀場巕娫偺岎屳嶌梡偼昁梫側尷傝抦偭偰偍偒傋偒偱偁傞乯傕専弌偱偒傞傛偆偵幚尡傪慻傓偙偲偑偱偒丆偦偺曽朄偲偟偰丆儔僥儞曽奿朄傗偦偺墑挿偱偁傞捈岎昞偵傛傞曽朄偑偁傝傑偡丏
丂椺偊偽丆悈堫偺廂検偵塭嬁傪媦傏偡場巕偼悢懡偔偁傝傑偡丏昳庬丆婥壏丆悈壏丆拏慺丆擔幩検丆嶌婜丆擔挿側偳側偳丏偙偺偡傋偰傪傕偟庢傝忋偘偰丆奺場巕偺悈弨傪俁偮偢偮愝偗偨偲偟偨傜丆偳偆側傞偱偟傚偆偐丏場巕偑俀偮側傜俁亊俁偱俋夞偺幚尡傪斀暅傪愝偗側偔偰傕偟側偗傟偽側傝傑偣傫丏場巕偑俁偮側傜丆俁俁偱俀俈偲側傝傑偡丏場巕偑係偮側傜俁係偱俉侾偲傕側傝丆悈堫偺幚尡偲偟偰偼傎偲傫偳晄壜擻偱偟傚偆丏
丂岺応偱傕偺傪嶌傞偲偒偵偼惂屼壜擻側場巕偼偐側傝偺悢偵側傝傑偡丏偦傟偧傟偺場巕偱嵟揔側悈弨傪尒偄偩偡偙偲偼惗嶻僐僗僩傪尭傜偟丆椙幙側惢昳傪嶌傞忋偱廳梫偱偡丏偟偨偑偭偰丆側傞傋偔懡偔偺場巕傪庢傝忋偘側偑傜丆幚尡夞悢傪彮側偔偡傞偙偲偑昁梫偱偡丏
侾丏懡尦攝抲偺暘嶶暘愅
丂擇尦攝抲偵傛傞暘嶶暘愅偺帪偵妛傫偩傛偆偵丆堦偮堦偮偺場巕傪暿乆偵幚尡偡傞偲暋悢偺場巕偑棈傫偩岎屳嶌梡偑専弌偱偒側偄偺偱丆摨帪偵偄偔偮偐偺場巕傪庢傝忋偘偰幚尡偡傞曽偑傛偄偙偲偼妋偐偱偡丏偟偐偟丆偁傑傝偵懡偔偺場巕傪摨帪偵庢傝忋偘傞偲幚尡悢偑憹偊偡偓偰丆尰幚揑偱偼偁傝傑偣傫丏
俁丏廻戣
俙丏師夞偐傜偼憡娭暘愅偲夞婣暘愅偵偮偄偰妛傇丏
丂憡娭暘愅偲偼俀偮偺曄検娫偺娭學偺嫮偝傪憡娭學悢偲偄偆抣傪媮傔偰挷傋傞曽朄偱偁傞丏夞婣暘愅偲偼俀偮偺曄検偺娭學偑偳偺偔傜偄偁傞偐傪掕検揑偵尒愊傕傝丆偝傜偵俀偮偺曄検偺娫偺娭學傪偁傞幃偵昞尰偡傞曽朄偱偁傞丏壓偵偼嶶晍恾乮俀偮偺曄検偺偆偪丆堦曽傪倶幉偵丆傕偆堦曽傪倷幉偵偟偰丆椉幰偺娭學傪恾帵偟偨恾乯偺僷僞乕儞偑偄偔偮偐偁傞丏倎偼倶偑憹偊傟偽丆倷傕憹壛偡傞孹岦偑偁傞娭學傪帵偡丏倎偺椺偲偟偰偼丆悽奅奺抧揰偱偺堦擭偺嵟崅婥壏偲嵟掅婥壏偵偼偙偺傛偆側娭學偑偁傞偩傠偆丏倕偼倶偑憹偊傟偽丆倷偼尭傞孹岦偺偁傞娭學傪帵偡丏倕偺椺偲偟偰偼丆堦擭娫偺惏揤偺擔悢偲崀悈検偺娭學偑嫇偘傜傟傞丏們偼倶偲倷偺娫偵娭學偑側偄偙偲傪帵偡丏們偺椺偲偟偰偼丆杒嬌偱偺僆乕儘儔偺悢偲搶嫗墂偱攧傟傞曎摉偺悢偑偁傞偐傕偟傟側偄乮偨傇傫娭學偼側偄偲偼巚偆偑ゥゥゥ乯丏
嘆丂埲忋偺倎丆們丆倕偺俁偮偺僷僞乕儞偵摉偰偼傑傞俀偮偺曄検傪峫偊傛丏
嘇丂倎傕偟偔偼倕偵僷僞乕儞偵偮偄偰丆20慻埲忋偺僨乕僞傪廤傔丆嶶晍恾傪彂偗丏
嘊丂嘇偱彂偄偨嶶晍恾傪尒偰丆俀偮偺曄検偺娭學偑偳偺掱搙嫮偄偺偐傪峫偊傛丏偡側傢偪塃偺恾偱傕倐傛傝偼倎偺曽偑椉曄悢偺娭學偑嫮偄丏帺暘偺廤傔偨僨乕僞傪塃偺僷僞乕儞偲斾妑偟丆偳傟偵嬤偄偐傪峫偊傛丏
奺帺偑堎側傞僨乕僞傪憡娭暘愅偲夞婣暘愅偺偦傟偧傟偵偮偄偰挷嵏偡傞偙偲丏偦偺偨傔偵帠慜偵偳偆偄偆僨乕僞傪挷嵏偡傞偐傪204幒慜偺儂儚僀僩儃乕僪偵揬偭偨巻偵曬崘偡傞偙偲乮憗偄幰彑偪偲偡傞乯丏崱夞偺廻戣偺採弌偼侾寧侾俇擔乮嬥乯屵屻俆帪偲偡傞丏
丂側偍嫍棧偲塣捓偺傛偆偵曅曽傪巜掕偡傞偲傕偆堦曽偑偽傜偮偒偑側偔丆寛傑偭偰偟傑偆僨乕僞偼偙偺傛偆側夝愅偵偼傆偝傢偟偔側偄丏搒摴晎導偺僨乕僞傪巊偆偺傕丆杒奀摴傗搶嫗搒偺傛偆偵柺愊傗恖岥偺嬌抂偵戝偒偄僨乕僞偑擖傞偺偱傛偔側偄丏